Cursus: Geometrija 1, tok 1o1

Algemeen

22 februari - 28 februari

Radili osnovno o vektorima ravni i prostora: neformalnu definiciju, sabiranje, množenje skalarom. Pokazali da su geometrijski vektori primer vektorskog prostora iz LA. Linearna (ne)zavisnost, dokazali da su svaka tri vektora ravni linearno zavisna.

Вежбе: Уведен је појам усмерене дужи, релације ~ међу усмереним дужима и вектора као класе еквиваленције скупа усмерених дужи. Објашњено је како се вектори сабирају и множе бројем (скаларом), наведене су особине ових операција. Објашњени су појмови линеарне независности и зависности вектора и урађен је први задатак из области Линеарне операције с векторима.

1 maart - 7 maart

Predavanja: koordinate vektora u bazi, matrica prelaska izmedju dve baze, veza koordinata preko matrice prelaska, definicija koordinata tačke u reperu, primeri, formule transformacije koordinata, transformacije koordinata ON repera u ravni, matrica rotacije i osobine, matrica simetrije i osobine, ortogonalne grupe SO(2) i O(2).

Вежбе: Урађени су задаци 1.2, 1.3, 1.4, 1.6. и 1.7. под а).

8 maart - 14 maart

Predavanja: skalarni proizvod, osobine skalarnog proizvoda, skalarni proizvod u ON bazi, primene skalarnog proizvoda na računanje uglova i dužina, merenje uglova (stepeni, radijani, procenti), vektorski proizvod, definicija vp, osobine vektorskog proizvoda, vp u ON+ bazi, primene vektorskog proizvoda u ravni (površina paralelograma, nastaviće se....)

Вежбе: Урађени задаци 1.10. 1.11 (Менелајева теорема), 1.12 (Чевина теорема) и 1.16.

15 maart - 21 maart

Predavanja: nastavili sa primenama vektorskog proizvoda (kolinearnost tri tačke, površina paralelograma i trougla, orijentacija trougla, da li tačka pripada trouglu), dvostruki vektorski proizvod, primer računanja dvostrukog proizvoda na dva načina, mešoviti proizvod: zapremina paralelopipeda, orjentacija baze prostora, osobine m.p., primer-primena mešovitog proizvoda na proveru komplanarnosti tačaka.

Вежбе: Урађени су задаци 1.17. и 1.19. Урађене су дефиниције и основне особине скаларног, векторског и мешовитог производа. Урађен је задатак 2.2. (доказ да се висине троугла секу у једној тачки коришћењем скаларног производа и Чевине теореме).

22 maart - 28 maart

Predavanja: počeli analitičku geometriju u prostoru, objasnili značenje koordinata, oktante, izveli jednačinu ravni kroz datu tačku sa datim normalnim vektorom, pričali o skiciranju ravni, segmentna jednačina ravni, ravan kroz tri tačke, parametarska jednačina ravni, parametarska jednačina prave, kanonska jednačina prave, primer ravni kroz dve tačke i podela duži na jednake delove.

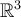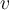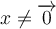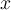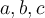Вежбе: Урађена теорема о симетрали угла и доказ да се симетрале унутрашњих углова секу у једној тачки (задатак 2.3). Урађени су обрасци за скаларни, векторски и мешовити производ у $\mathbb{R}^3$ . Урађено је нормално пројектовање вектора $v$ на вектор $x \neq \overrightarrow{0}$ (задатак 2.4) и израчунавање вектора $x$ преко $a, b, c$ ако су познате вредности скаларних производа $\langle x, a\rangle$ , $\langle x, b\rangle$ , $\langle x, c\rangle$ .

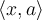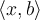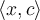29 maart - 4 april

Predavanja: prava kao presek dve ravni, pramen ravni, rastojanje tacke od prave, rastojanje tacke od ravni

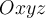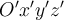Вежбе: Завршена је област Скаларни, векторски и мешовити производ. Урађени су задаци 2.11, 2.12, 2.13. и 2.14. Започета је област Трансформације координата. Објашњено је како се долази до обрасца за прелазак из координатног система $Oxyz$ у $O'x'y'z'$ изражавањем базних вектора координатног система 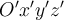$O'x'y'z'$ и вектора 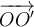$\overrightarrow{OO'}$ помоћу базних вектора координатног система 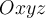$Oxyz$ . Урађен је задатак 3.1.

5 april - 11 april

Predavanja: medjusobni polozaji: dve ravni, prave i ravni, dve prave, zajednička normala mimoilaznih pravih, rastojanje mimoilaznih pravih, ugao izmedju dve prave, ugao izmedju prave i ravni, ugao izmedju dve ravni, primer (ugao izmedju pljosni pravilnog tetraedra).

Вежбе: Урађени су задаци 3.3. и 3.6. (с правоугаоником и коцком). Објашњено је да је координатни систем правоугли ако су координатни вектори међусобно нормални, а Декартов ако је сваки координатни вектор дужине 1. Објашењено је како се може користити тригонометријски круг за проналажење ортонормираног репера у равни (било које оријентације) и како се може користити векторски производ да се нађе трећи координатни вектор ортонормираног репера (Декартовог правоуглог координатног система) позитивне оријентације.

12 april - 18 april

Predavanja: ugao izmedju pljosni pravilnog tetraedra (drugi način), konusni preseci, konike, teorema o žiži i direktrisi, ekscenticitet (e) u zavisnosi od položaja presečne ravni i konusa, polarna jednačina konike, dokaz da je za e=1 konika parabola.

Dokaz da je za e<1 konika elipsa (za e=0 krug), a za e>1 hiperbola nismo radili na času, ali ga imate u beleškama.

Вежбе: Координате тачака у Декартовом правоуглом координатном систему 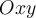$Oxy$ у равни. Једначина праве у равни (канонски облик, параметарски облик, имплицитни облик). Вектор правца праве. Израчунавање угла између двеју правих и одређивање симетрале угла који заклапају две праве. Растојање тачке од праве. Једначина круга у равни. Тангента круга. Заједничке тангенте два круга у равни. Поларне координате у равни. Урађени су задаци 4.1, 4.2, 4.3, 4.4. и 4.7.

19 april - 25 april

Predavanja: objasnjeno (detalji u beleškama od prošle nedelje) da se za 0<e<1 dobija elipsa, za e>1 hiperbola, a za e=0 krug. Osnovne osobine i "formule" elipse, hiperbole i parabole, fokalne osobine elipse i hiperbole, "konstrukcija" elipse i hiperbole, putanja kosog hica je parabola, maksimalni domet, uraditi primer, Keplerovi zakoni.

Вежбе: Једначина праве и равни у простору. Међусобни положај правих у простору. Угао између двеју правих, праве и равни и двеју равни. Проналажење тачке симетричне датој тачки у односу на дату раван. Проналажење заједничке нормале мимоилазних правих.

26 april - 2 mei

Predavanja: tangente konika, optičke osobine konika, krive drugog reda (primeri), krive drugog reda (klasifikacija)

Вежбе: Криве другог реда: жиже, директрисе, осе, ексцентрицитет; центар елипсе и хиперболе, параметри елипсе и хиперболе, асимптоте хиперболе; веза између параметара; конјуговани правци код елипсе и хиперболе. Урађени су задаци 5.1, 5.3, 5.4, 5.6, 5.8. и 5.11.

3 mei - 9 mei

Predavanja: nismo imali zbog praznika

Вежбе: Урађени су задаци 5.13. и 5.14. Објашњен је поступак свођења криве другог реда на канонски облик и урађен је задатак 5.16.

Уведен је појам афиног пресликавања. Објашњена је сличност са трансформацијама координата. Објашњено је каква је веза афиних и линеарних пресликавања. Објашњено је шта су изометрије, када афина пресликавања чувају површину (у равни, односно запремину у простору) и оријентацију. Урађени су задаци 6.1. и 6.3.

10 mei - 16 mei

Predavanja: radili svodjenje krive drugog reda na kanonski oblik (pokazali dva načina kroz primer, prvi način: rotacijom, drugi način: sopstvenim vektorima), uveli pojam konjugovanih dijametara elipse, izveli formule centra krive drugog reda preko parcijalnih izvoda.

~~25. maja imate test iz Afinih preslikavanja. Više detalja u Obaveštenjima.~~

Вежбе: Урађена је осна рефлексија равни, хомотетија равни, скалирање по осама (задаци 6.5, 6.6. и 6.8). Урађена је раванска рефлексија простора, централна симетрија и хомотетија простора (задаци 6.7, 6.10. и 6.12). Објашњено је како се криве у простору добијају као пресек двеју површи. Показано је како се од дате криве и ненула вектора формира цилиндар (унија свих правих које имају правац као дати вектор и садрже неку тачку задате криве). Урађени су задаци 7.1. и 7.2. (није завршен).

17 mei - 23 mei

Predavanja: površi drugog reda, kanonski oblici, crteži, dokaz da je presek površi drugog reda i ravni kriva drugog reda, pravolinijske površi, jednograni hipeboloid je dvostruko pravolinijska površ (dokaz), parabolički hiperboloid je dvostruko pravolinijska površ.

Geometrija sfere, veliki krugovi na sferi, "dokaz" da je najkraća kriva između dve tačke na sferi kraći luk velikog kruga.

Вежбе: Проналажење тангентних равни сфере и симетралних равни диедара одређених тим равнима (задатак 7.2), уписивање сфере у кружни конус (задатак 7.3), проналажење површи која представља геометријско место тачака на једнаком растојању од двеју мимоилазних правих (задатак 7.7), проналажење цилиндра описаног око сфере на два начина (задатак 7.8), проналажење конуса којег одређују дата крива и дата тачка као врх конуса (задатак 7.10), проналажење кружног конуса с датом осом и тангентном равни (задатак 7.11) и проналажење конуса који додирује дату сферу (задатак 7.12 - није довршен).

24 mei - 30 mei

Predavanja (poslednji čas): radili sfere trouglove, geografske koordinate, sfernu kosinusnu teoremu, računanje rastojanja između tačaka na površini Zemlje, sinusnu sfernu teoremu, površinu sfere, pokazali da je zbir uglova sfernog trougla uvek veći od opruženog ugla.

Test iz afinih preslikavanja zakazan za 25. maj se NEĆE održati iz tehnničkih razloga! Izvinjavam se zbog promene plana. Afina preslikavanja odgovarate na usmenom (ukoliko ih dobijete kao ispitno pitanje). Literatura - tri YouTube snimka.

Вежбе: Урађени су задаци 7.12, 7.13. и 7.14. под 2). Објашњено је како се гледа сенка сфере када је извор светлости у врху конуса који додирује сферу, а платно је нека раван, као и да је сенка унутрашњост криве у пресеку конуса и равни, а контура сенке (граница између осенченог и неосенченог дела) крива у пресеку конуса и равни. Објашњено је како се тражи нормална пројекција криве на координатне равни и како се изводи свођење површи другог реда на канонски облик. Уведени су основни појмови сферне геометрије, објашњено је да се најкраће растојање између тачака на сфери добија када се иде по великом кругу сфере који садржи дате тачке. Уведен је појам сферног троугла, објашњено је шта су његови елементи, наведене основне једнакости и неједнакости које сферни троугао задовољава. Урађени су задаци 8.1, 8.3, 8.5 и 8.6.

--- КРАЈ КУРСА ---

Overzicht van de weken