Пети домаћи задатак
1. (2 п) Нека су 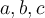 дати вектори у простору. Доказати да су они линеарно независни ако и само ако су вектори
дати вектори у простору. Доказати да су они линеарно независни ако и само ако су вектори 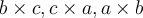 линеарно независни.
линеарно независни.
2. (2 п) Одредити вектор 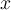 ако важи
ако важи 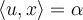 и
и 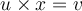 , за дате векторе
, за дате векторе 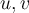 и дати реални број
и дати реални број 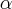 .. Дискутовати све могуће случајеве.
.. Дискутовати све могуће случајеве.
3. (1 п) Дат је троугао 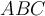 површине
површине 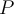 . Нека су тачке
. Нека су тачке 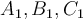 такве да важи
такве да важи 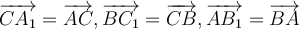 . Колика је површина троугла
. Колика је површина троугла 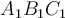 ?
?
4. (2 п) Дате су две праве пирамиде с истом основом, квадратом 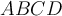 ивице
ивице 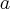 . Нека су
. Нека су 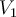 и
и 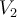 врхови датих пирамида и угао између правих
врхови датих пирамида и угао између правих 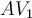 и
и 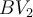 једнак
једнак  . Ако је висина једне пирамиде једнака
. Ако је висина једне пирамиде једнака 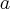 , одредити висину друге пирамиде.
, одредити висину друге пирамиде.