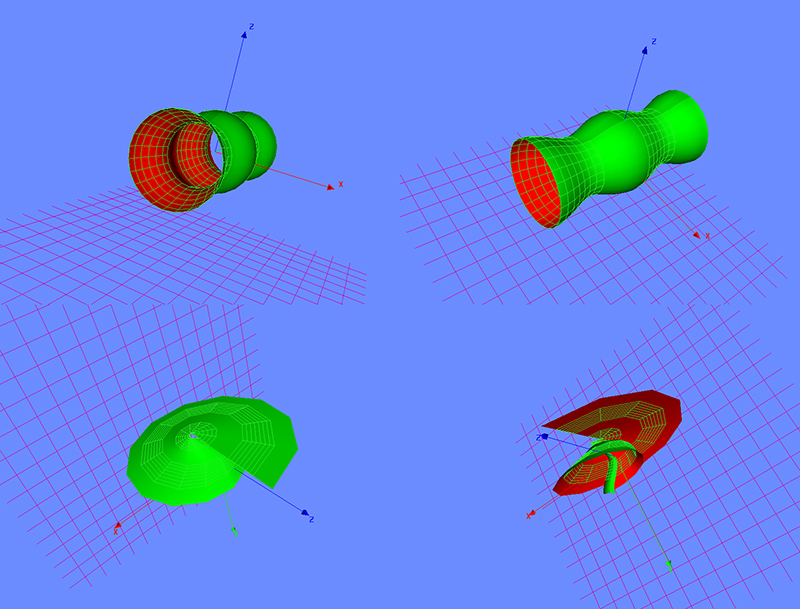
a)
X=sqrt((cos(u))^2 + (1)^2)*sin(v)
Y=u
Z=sqrt((cos(u))^2 + (1)^2)*cos(v)
0<=u<=2*pi
0<=v<=4*pi
X=cos(u)
Y=u
Z=1
0<=u<=2*pi
rotacija oko Y ose
b)
X=(4*pi - v)/(4*pi - 0) * cos(u) + (u - 0)/(2*pi - 0) * v*sin(v)
Y=(4*pi - v)/(4*pi - 0) * u + (u - 0)/(2*pi - 0) * 1
Z=(4*pi - v)/(4*pi - 0) * 1 + (u - 0)/(2*pi - 0) * v*cos(v)
cosinus
X=cos(s)
Y=u
Z=1
helix
X=v*sin(v)
Y=1
Z=v*cos(v)
0<=U<=2*pi
0<=V<=4*pi