MAT 04 - Rotacione i translatorne površi
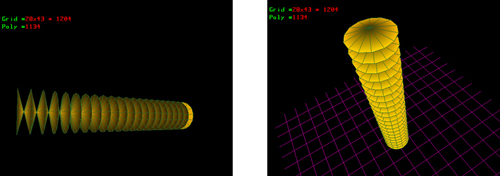
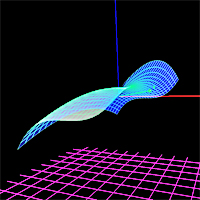
Graficki prikazati povrs koja se dobija rotacijom parametarski definisane krive oko izabrane ose.
U ovom zadatku koristiti neki od ranije koriscenih programa ili K3D Surf (Tools, Builder, Revolve...; kontrola boje: Options; Kontrola prikaza: Parametric, Drawing Options).
U tekstualnom delu zadataka dati parametarsku jednacinu krive linije, navesti osu oko koje rotira ova linija, kao i granice parametara u i v.
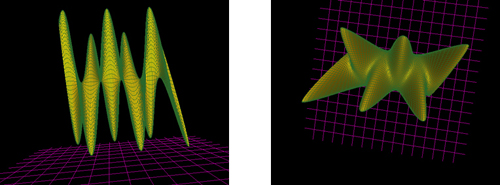
Kao reply na taj post graficki prikazati povrs koja se dobija translatornim kretanjem parametarski definisane krive linije duz neke druge linije.
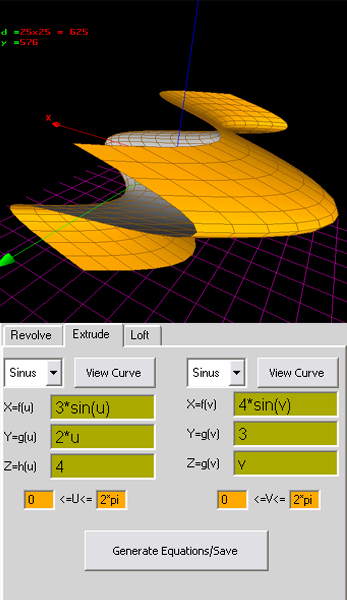
Koristiti takodje K3D Surf (Tools, Builder, Extrude...; kontrola boje: Options; Kontrola prikaza: Parametric, Drawing Options).
U tekstualnom delu zadatka dati parametarski oblik obe linije, kao i granice parametara u i v.
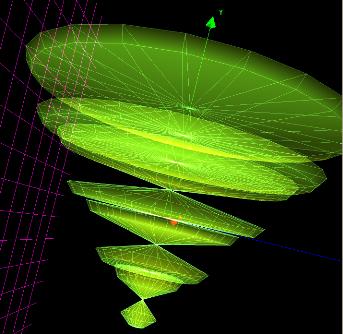
parametri:
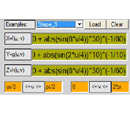
x: 5*sin(u)+cos(tan(2*u))
y: u+sin(u)
z: 2
rotacija oko Y-ose
granice: 0<=u<=2*pi

ja ne znam da li je ovo dobro...radila sam u 3d grapher-u jer nisam uspela da skinem k3d surf
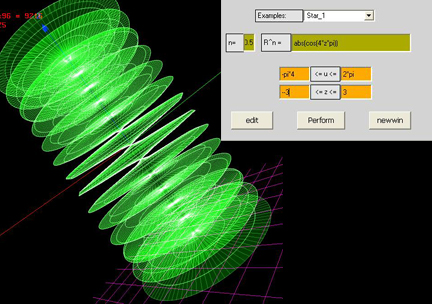
cylindrical
a=sin(4*v)
R=5*cos(v)*sin(u)
Z=v
-20<u<40 steps 35
-5<v<30 steps 40

K3DSurf
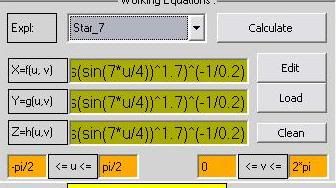
parametri:
x: cos(u)
y: 2*sin(7*u)*sin(u)
z: 2*cos(u)
rotacija oko Z-ose
granice: 0<=u<=2*pi
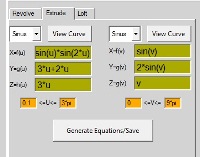
Y = sin(u)*sin(2*v)
Z = sin(v)-u
With U[ 0, 2*pi] And V[ -pi/2, pi/2]

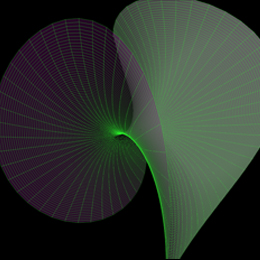
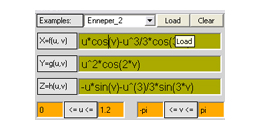
y=u^2*cos(2*v)
z=u*sin(t)-u^(6)/3*sin(4+v)
0.6=u=1.2 -3*pi=v=pi
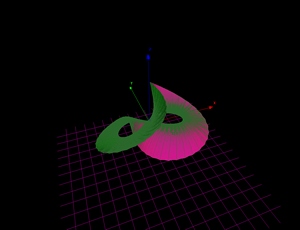
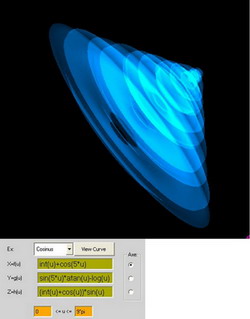
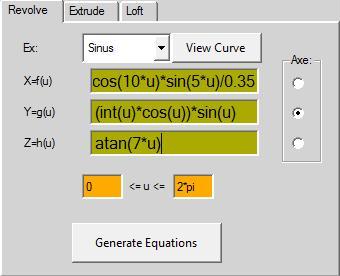
y=(int(u)+cos(u))*sin(u)
z=atan(5*u)
rotacija oko y-ose
0<=u<=2*pi

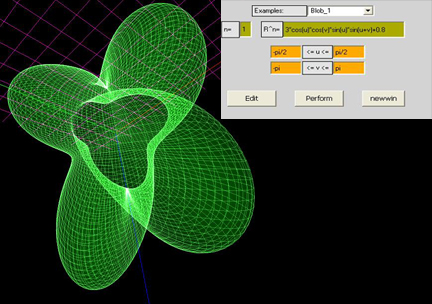
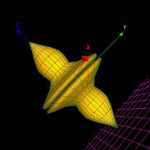
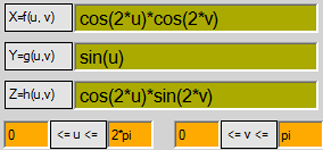
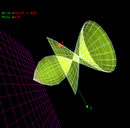
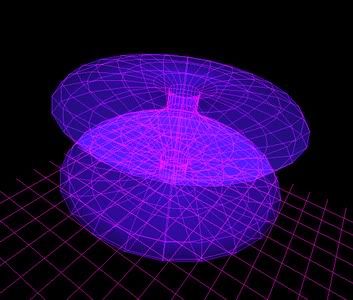
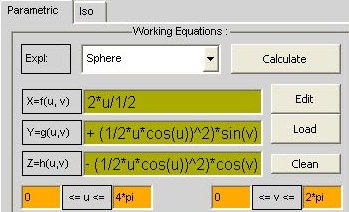
povrs:
x=f(u,v)=cos(2*u)*cos(2*v)
y=g(u,v)=sin(u)
z=h(u,v)=cos(2*u)*sin(2*v)
dobija se rotacijom krive:
x=f(u,v)=cos(2*u)
y=g(u,v)=sin(u)
z=h(u,v)=1
oko y-ose.


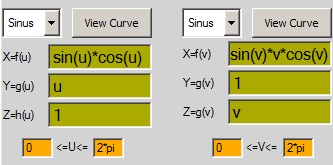
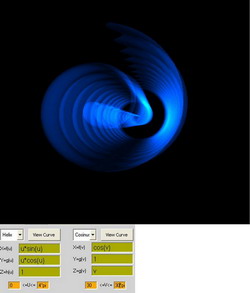
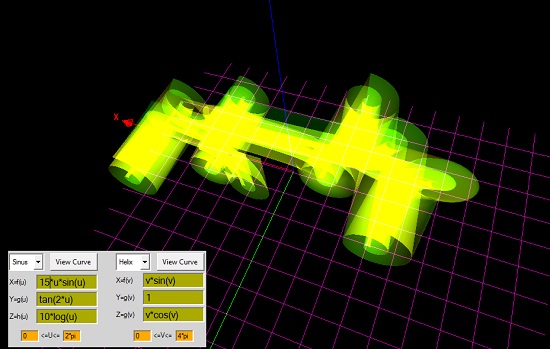
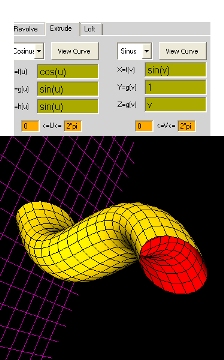
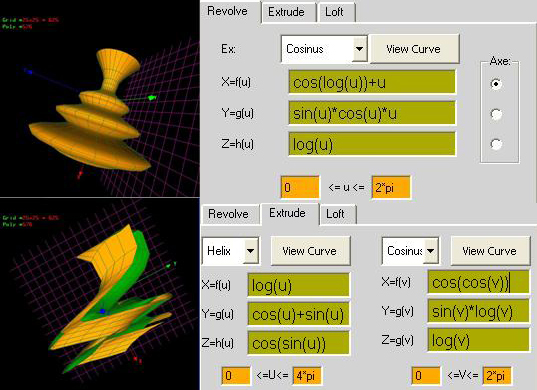
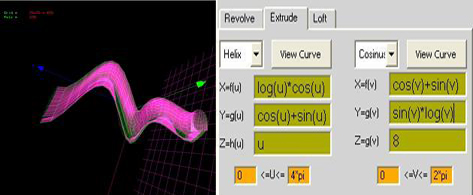
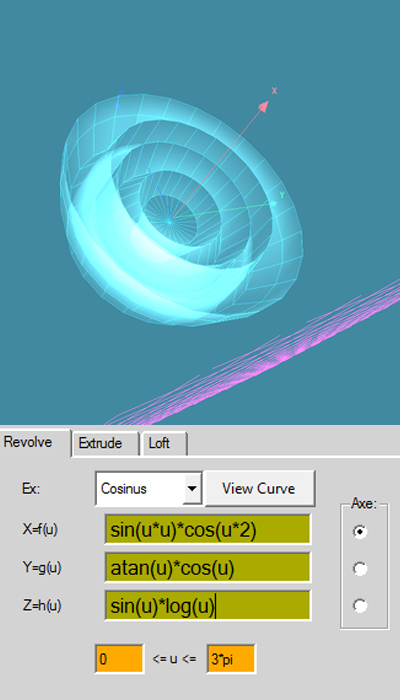
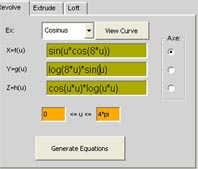
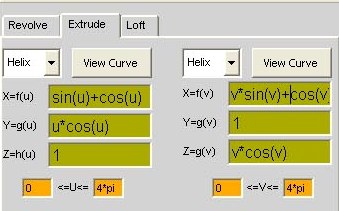
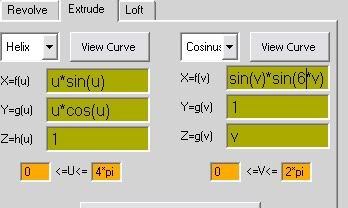
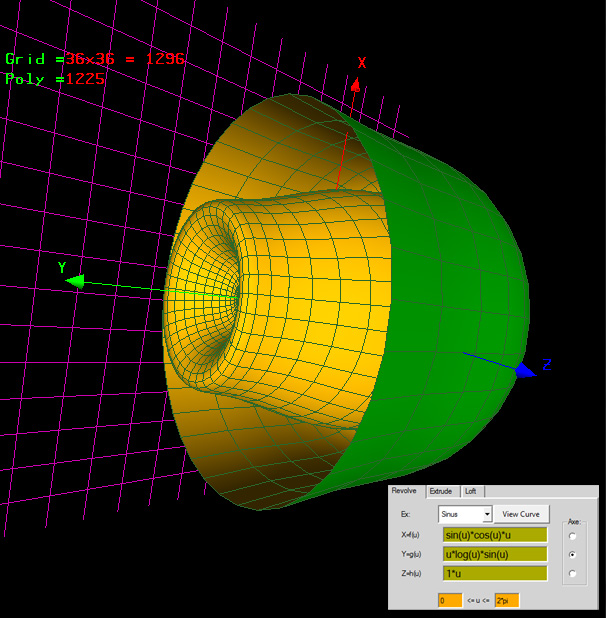
xf(u)=cos(u) xf(v)= v*sin(v)
yg(u)=u*cos(u) + 1 yg(v)=1
zh(u)=log(u)*log(u) zg(v)=v*cos(v)
u: 0 - 4*pi v: 0 - 2*pi
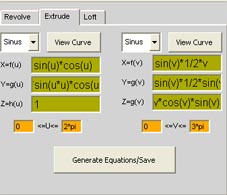
x=1*cos(v)-sin(v)*1, y=1*cos(v)+sin(v)*1, z=v
x=1.5*cos(v)-sin(v)*1.5, y=1.5*cos(v)+sin(v)*1.5, z=v
x=2*cos(v)-sin(v)*2, y=2*cos(v)+sin(v)*2, z=v
x=2.5*cos(v)-sin(v)*2.5, y=2.5*cos(v)+sin(v)*2.5, z=v
x=3*cos(v)-sin(v)*3, y=3*cos(v)+sin(v)*3, z=v
x=3.5*cos(v)-sin(v)*3.5, y=3.5*cos(v)+sin(v)*3.5, z=v
x=4*cos(v)-sin(v)*4, y=4*cos(v)+sin(v)*4, z=v
x=4.5*cos(v)-sin(v)*4.5, y=4.5*cos(v)+sin(v)*4.5, z=v
x=5*cos(v)-sin(v)*5, y=5*cos(v)+sin(v)*4, z=v
MinU=-10 MaxU=10 Steps=100
MinV=-10 MaxV=10 Steps=100
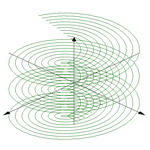
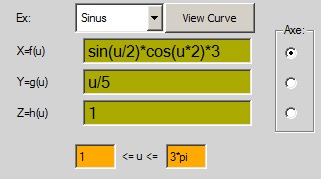
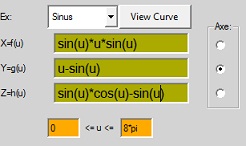
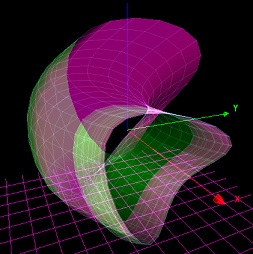
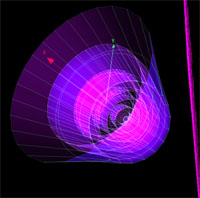
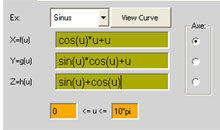
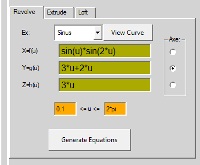
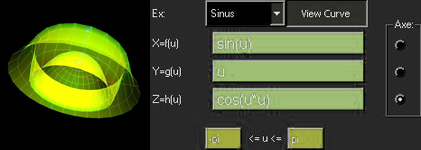
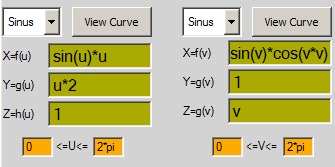
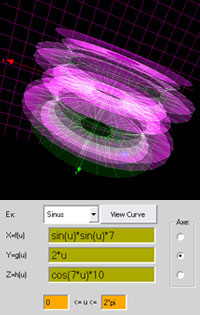
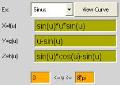
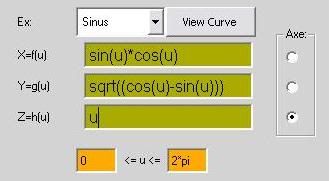
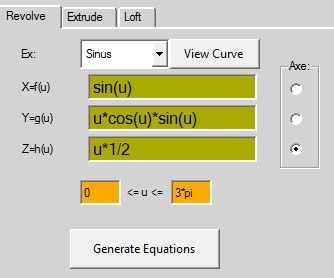
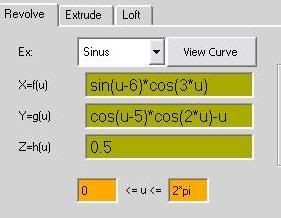
ex: sinus
x=f(u)= sin(u)*cos(u)*12
y=g(u)= atan(u)*2
z=h(u)= atan(u)-sin(u)*5
15*pi
rotacija oko z ose
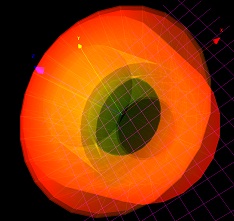
Parametri:
X=f(u)=u*cos(u/2)
Y=g(u)=cos(u/2)*sin(2*u)*u
Z=h(u)=u*sin(u)
Granice:
-1<=u<=2*pi
Rotacija oko Z ose

Y=g(u) 1.5*sin(u)*10*cos(u)
Z=h(u) 3*cos(u)
10<=u<=5*pi
axe Y2*pi<=v<=10*pi7

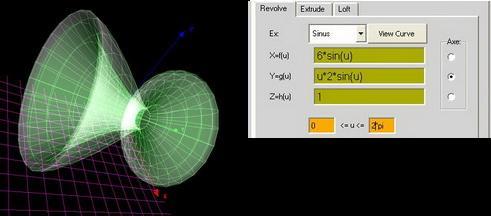
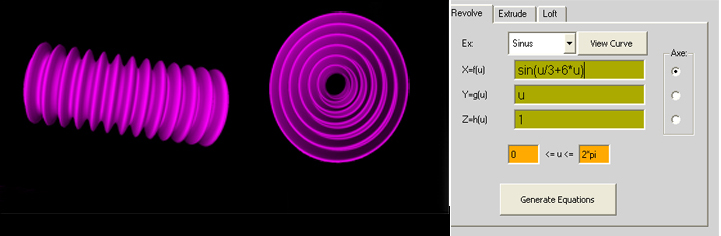
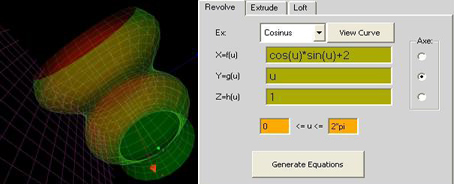
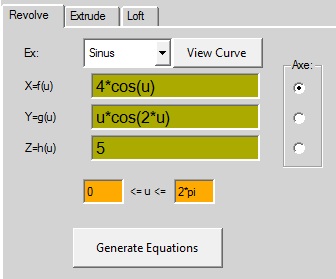
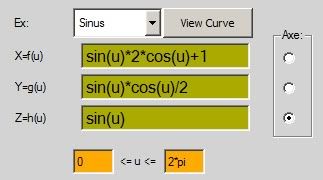
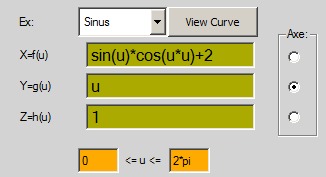
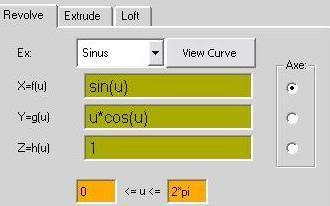
ex: sinus
x=sin(u)+cos(2*u)
y=u*sin(u)
z=1
0=u=2*pi

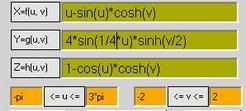
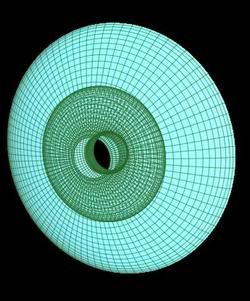
Yg(u)=u*sin(v/2)
Zh(u)=sin(v)+u*cos(v/2)*sin(v)
0*pi<v<2*pi
rotacija je oko z-ose
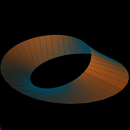
povrs:
x=f(u,v)=cos(2*u)*cos(2*v)
y=g(u,v)=sin(u)
z=h(u,v)=cos(2*u)*sin(2*v)
dobija se rotacijom krive:
x=f(u,v)=cos(2*u)
y=g(u,v)=sin(u)
z=h(u,v)=1
oko y-ose

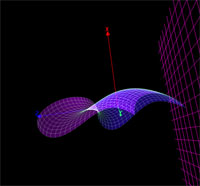
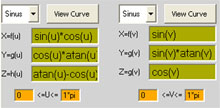
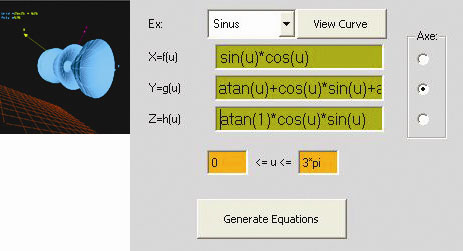
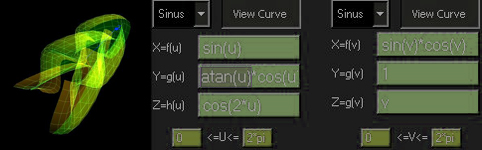
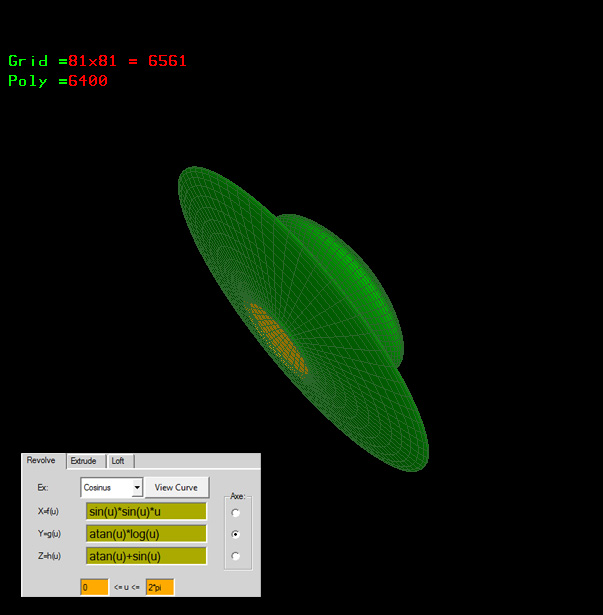
Xf(u)= sin(u)*cos(u)
Yg(u)= atan(u)+cos(u)*sin(u)+atan(1)*cos(u)*sin(u)
Zh(u)= atan(1)*cos(u)*sin(u)
0*pi
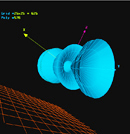
a(u,v,t) = cos(v)
R(u,v,t) = sin(v)*cos(u)
Z(u,v,t) = sin(u)-cos(v)
rotacija oko Z ose
Domen
MinU: -3.1415 MaxU: 3.1415 Steps: 30
MinV: -3.1415 MaxV: 3.1415 Steps: 40

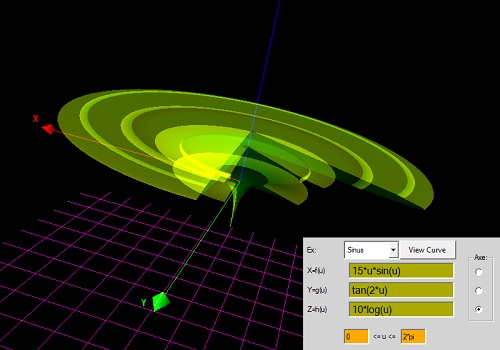
X=f(u) cos(u)*5*sin(u)
Y=g(u) u*cos(4*u)
Z=h(u) cos(u)-sin(u)
0 <= u <= 2*pi
rotira oko Y-ose

Ex:sinus
rotira oko z ose
x=15*sin(3*u)*u
y=2*cos(u^4)+5*u
z=32*sin(u)*sin(u)+26*sin(u)
u se nalazi izmedju nula i 2pi. (iz nepoznatog razloga,ovaj parametar se izbrise svaki put kada stavim znak za vece ili jednako)
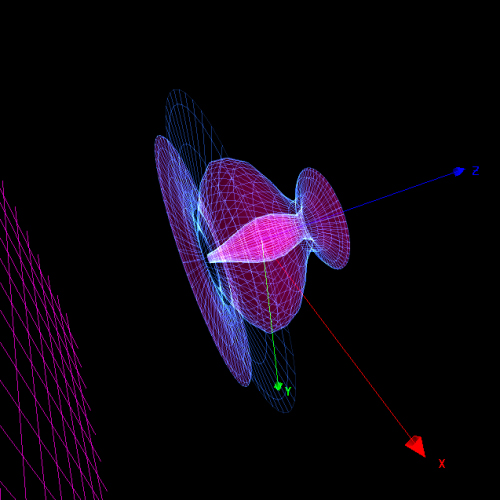
x=f(u)=2*sin(u)+2*cos(u)
y=g(u)=u/2
z=h(u)=log(u*u)
u od pi/2 do 2*pi
Rotacija po z-osi

y=g(u) sin(u)*cos(u)*cos(u)*sin(u)
z=h(u) u+1
0-2*pi

Parametri:
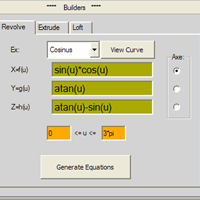
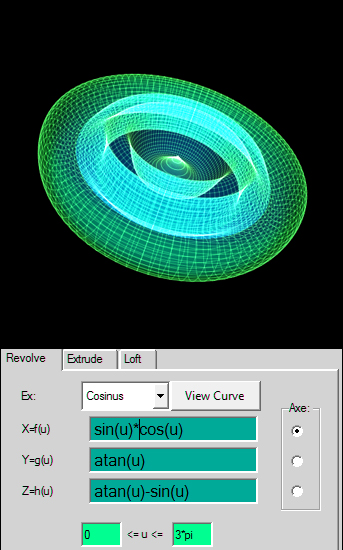
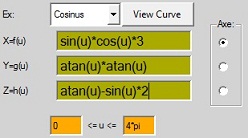
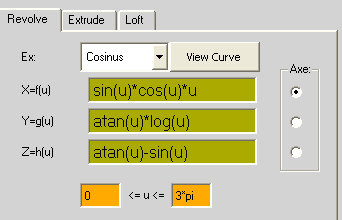
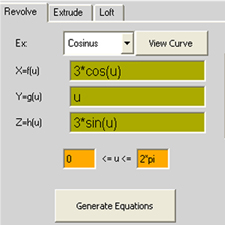
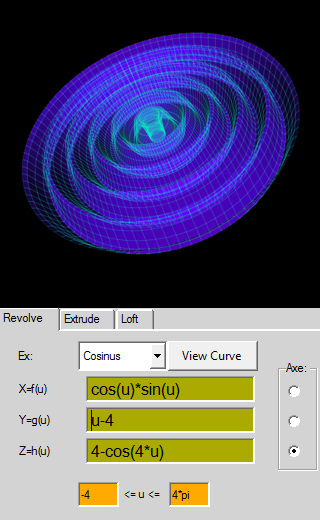
Ex: Cosinus
Xf(u)= sin(u)*cos(u)
Yg(u)= atan(u)*sin(u)*cos(u)
Zh(u)= atan(u)-sin(u)
0*pi<u<3*pi
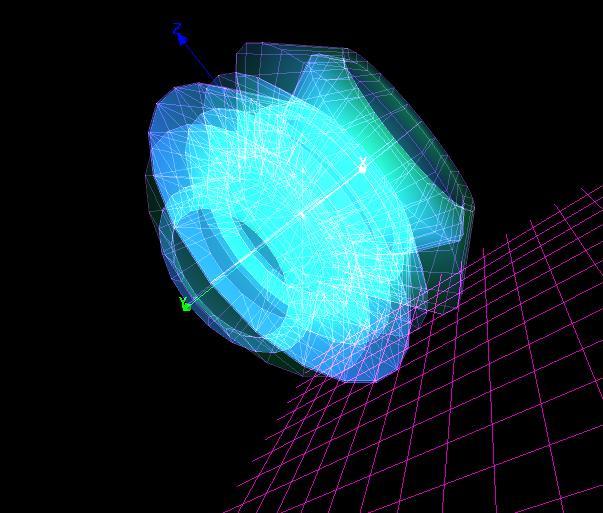
rotacija oko z-ose
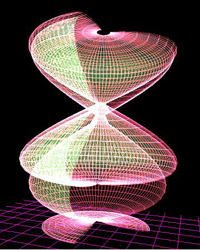
KD3Surf
X=v*2*cos(u)
Y=v*sin(u)
Z=v^2
0<=u<=2*pi
0<=v<=2
rotira oko x-ose
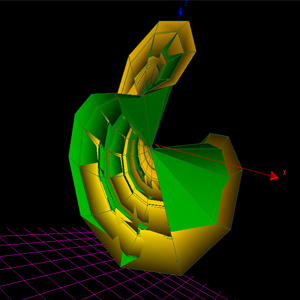
bilo mi je zanimljivo da rad prikazem iz vise uglova

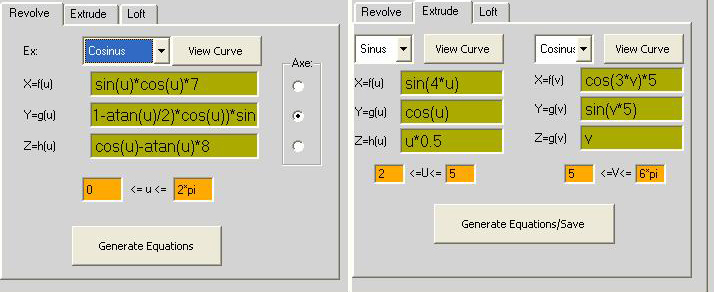
x=sin(u)*cos(u)*7
y=(4+2*(1-atan(u)/2)*cos(u))*sin(u)
z=cos(u)-atan(u)*8
0 <= u <=2*pi
extrude:
x=f(u) sin(4*u)
y=g(u)cos(u)
z=h(u)u*0.5
2<=u<=5
x=f(v)cos(3*v)*5
y=g(v)sin(v*5)
z=h(v)v
5<=v<=6*pi
rotira oko z-ose
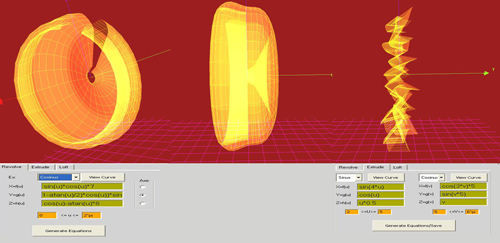
K3dsurf
x=sin(u*2)+cos(u)
y=u*2-sin(u)+atan(u)
z=sin(u)-atan(u)*cos(u*6)
od 0 do 2pi
rotacija oko z ose

k3dsurf
x=u/2
y=cos(u)+cos(u)+sin(u)+sin(u)
z=1/9*u-sin(u)+cos(u)+cos(u)+cos(u)
rotacija oko y ose
granice 0<=u<=2*pi

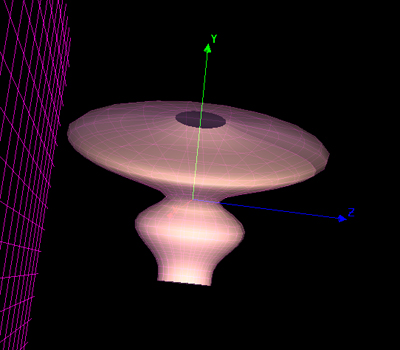
K3DSurf
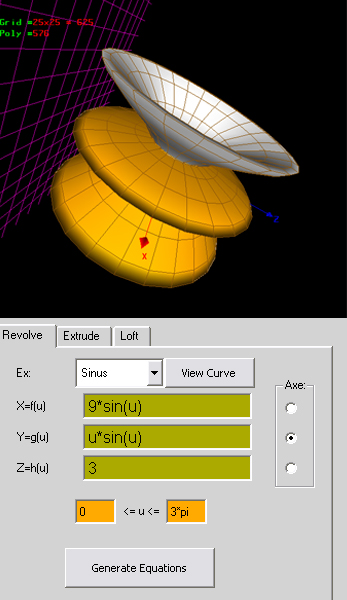
Revolve
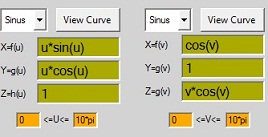
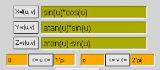
X=sin(U)
Y=U
Z=1
0<=U<=2*Pi
X Osa
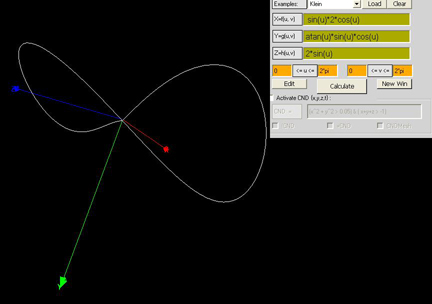
Parametric curve
X=sin(u)
Y=sqrt((u)^2 + (1)^2)*sin(v)
Z=sqrt((u)^2 + (1)^2)*cos(v)
0<=U<=2*Pi
0<=V<=2*Pi
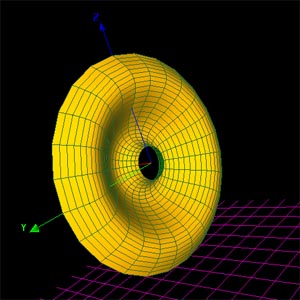
x=(2*(cos(u) + u*sin(u))*sin(v))/(1+ u^2*sin(v)^2)
y=log(tan(1/2 *v)) + (2*cos(v))/(1+ u^2*sin(v)^2)
z=(2*(sin(u) - u*cos(u))*sin(v))/(1+ u^2*sin(v)^2)
0<=u<=2*pi 0.01<=v<=pi-0.01
rotacija oko z-ose
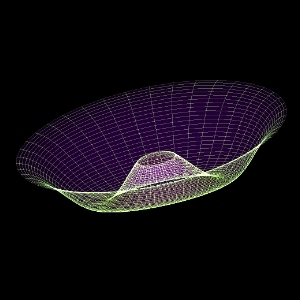
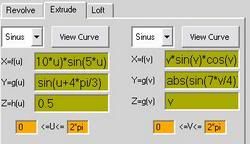
X=f(u,v) : (1-sqrt(u*u + v*v) / sqrt(2*pi*pi))*cos(u)*cos(v)+sqrt(u*u + v*v) / sqrt(2*pi*pi)*sin(u)*sin(v)
Y=g(u,v): (1-sqrt(u*u + v*v) / sqrt(2*pi*pi))*cos(u+4*pi/3)*cos(v+4*pi/3)+sqrt(u*u + v*v) / sqrt(2*pi*pi)*sin(u+4*pi/3)*sin(v+4*pi/3)
Z=h(u,v): qrt(u*u + v*v) / sqrt(2*pi*pi))*cos(u+2*pi/3)*cos(v+2*pi/3)+sqrt(u*u + v*v) / sqrt(2*pi*pi)*sin(u+2*pi/3)*sin(v+2*pi/3)
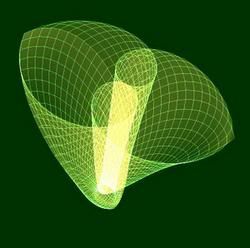
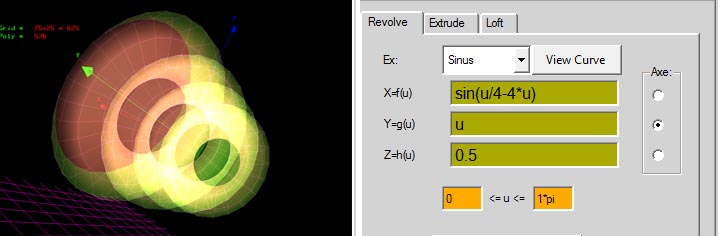
x=f(u): u*cos(u)
y=g(u): 0.8 * (u*sin(u) * sin((u*cos(u) - -1)*2*pi*1/2) + u * cos((u*cos(u) - -1)*2*pi*1/2))
z=h(u): 0.5
0<=u<=2*pi
1.oko x ose
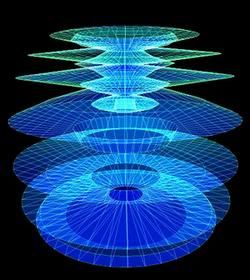
2.oko y ose

y: sin(3*sqrt(u))-cos(2*u)
z: cos(u)*sin(u)+cos(3*u)
rotacije oko z ose
1.5<=u<=2*pi

x=f(u) u*sin(u)
Y=g(u) cos(u)*atan(u)
Z=h(u) u*atan(u)
granice: 0<=u<=2*pi
rotacija oko Z ose
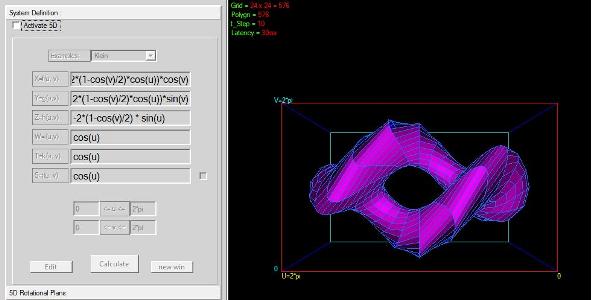
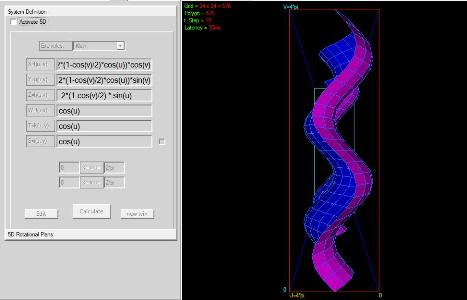
Y=g(u,v) 4+2*(1-cos(v)/2)*cos(u))*sin(v)
Z= h(u,v) -2*(1-cos(v)/2) * sin(u)
0<=u<=2*pi 0<=v<=2*pi
rotira oko y-ose
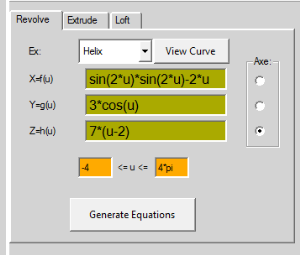
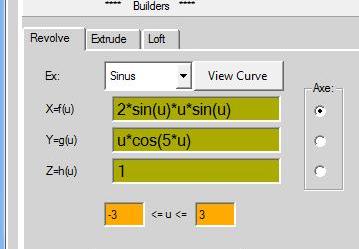
Yg(U)=2*sin(7*u)*sin(u)
Zh(U)=2*cos(u)
0<= u <= 3*pi

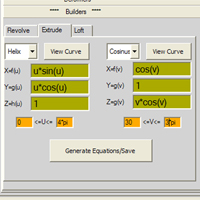
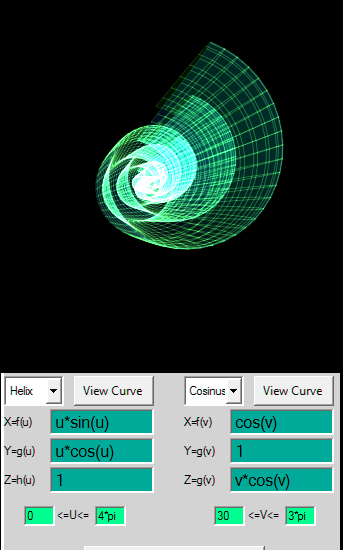
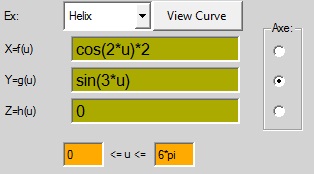
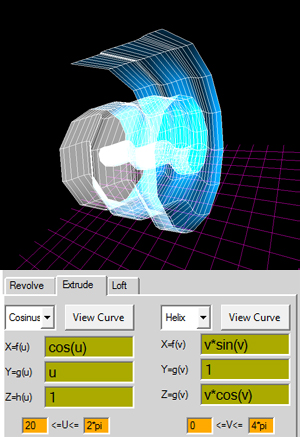
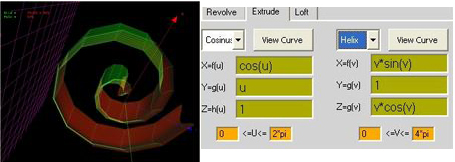
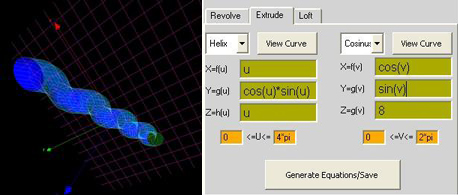
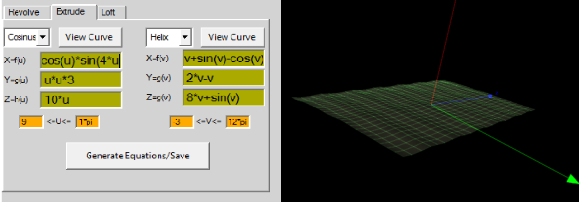
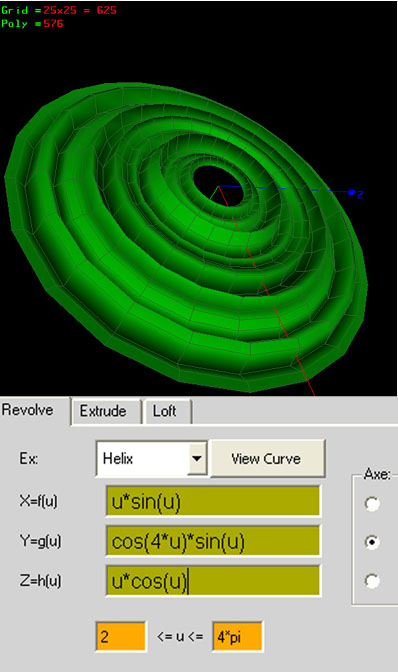
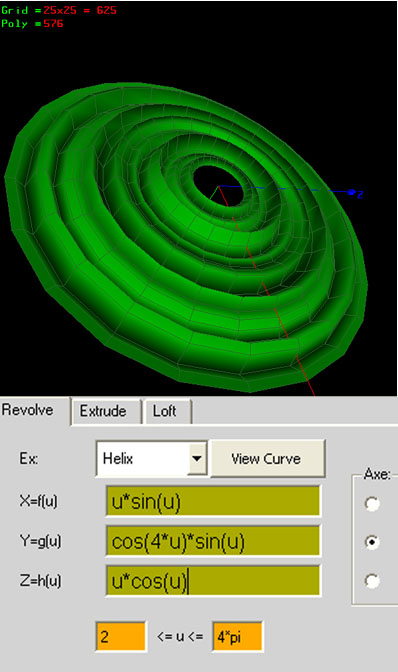
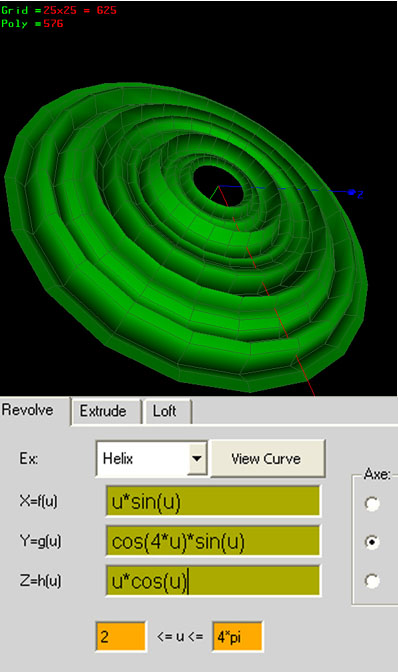
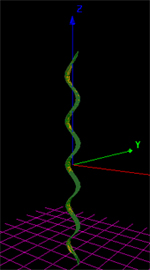
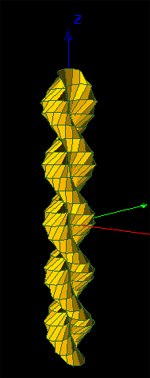
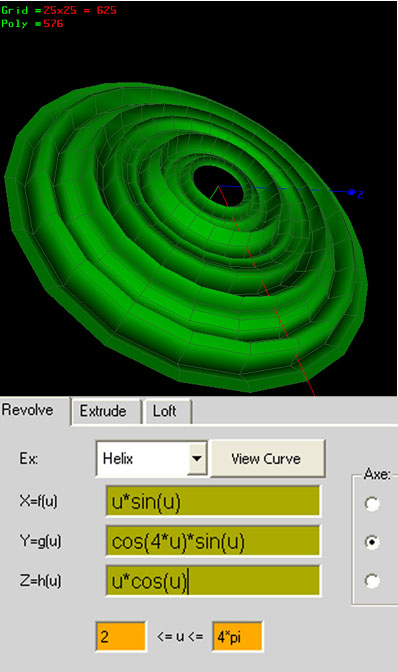
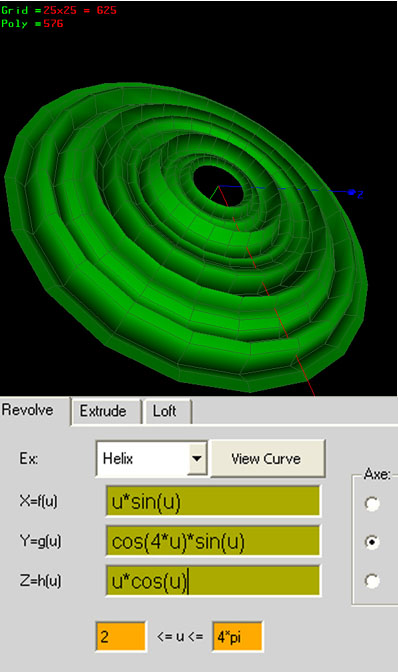
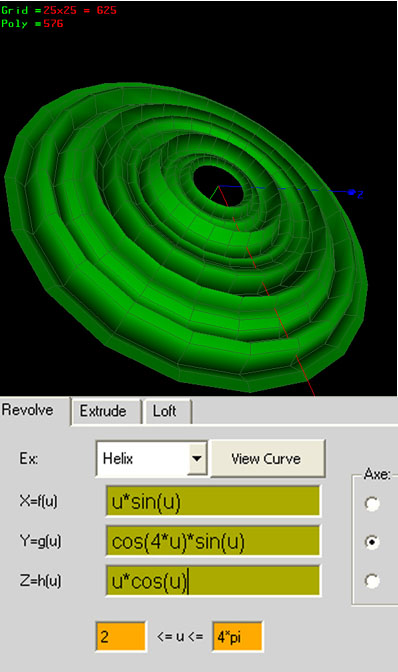
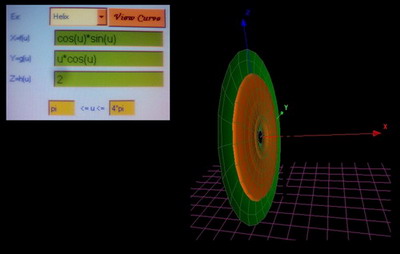
ex: Helix
X=f(u) =u
Y=g(u) =cos(u)
Z=h(u) =1
0<=u<=4*pi
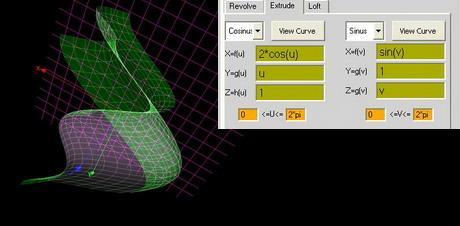
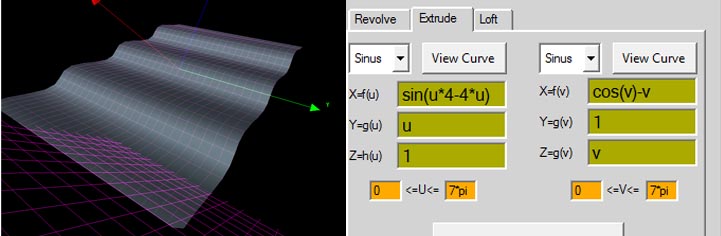
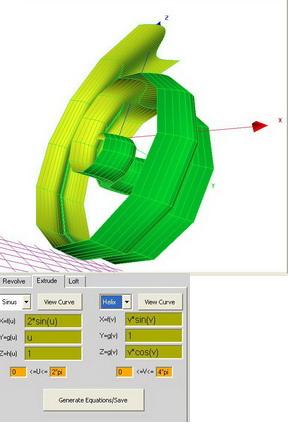
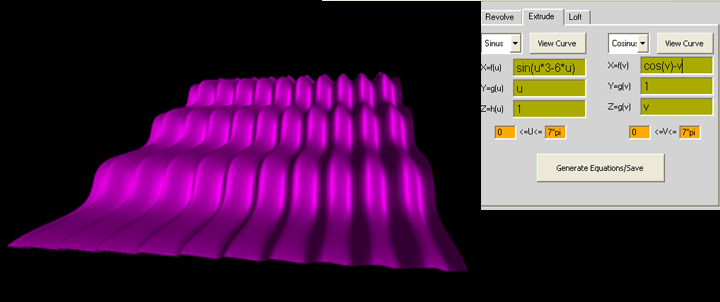
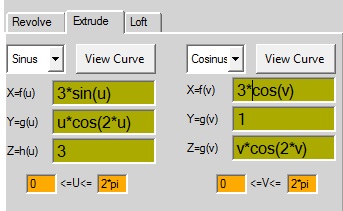
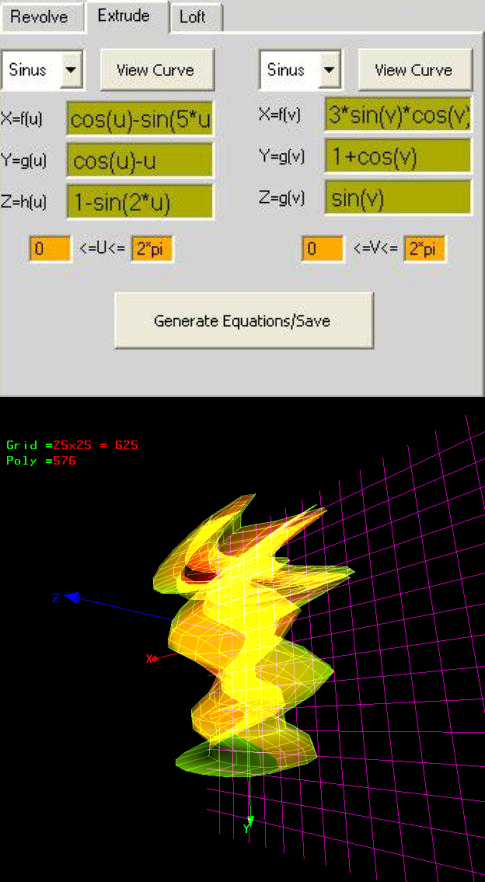
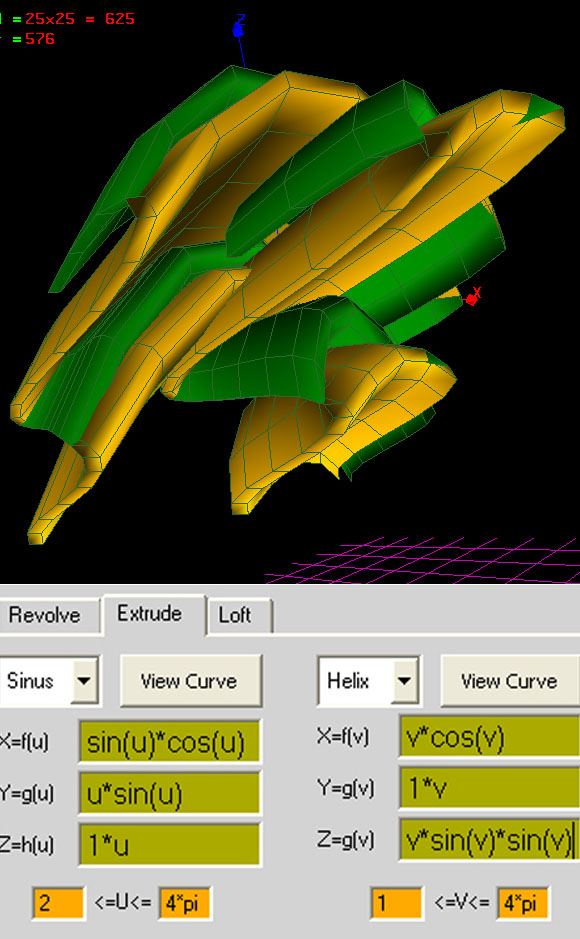
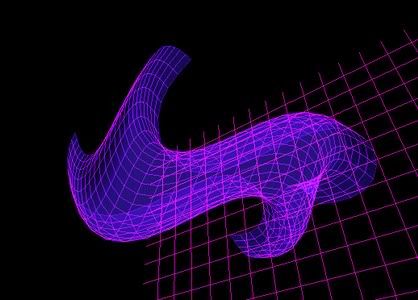
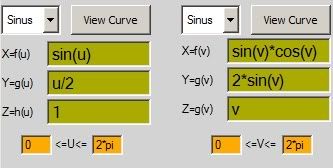
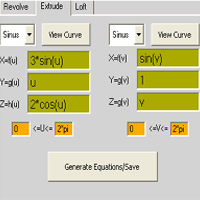
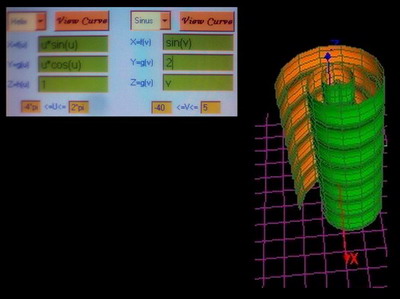
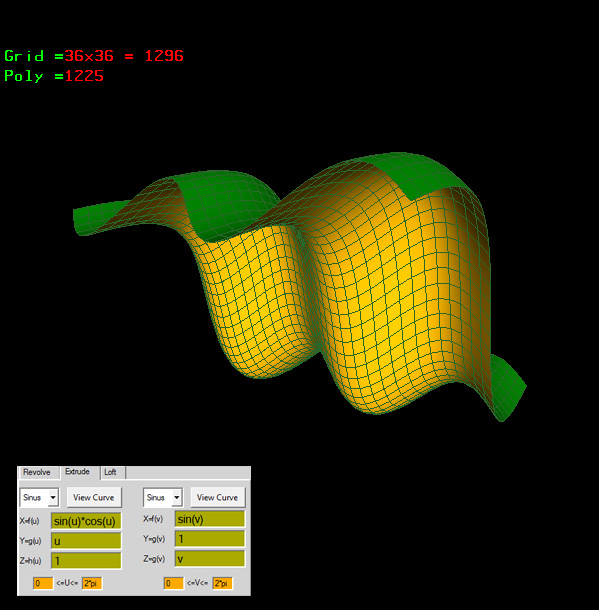
extrude
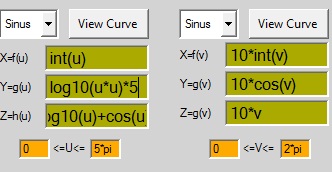
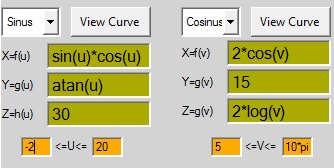
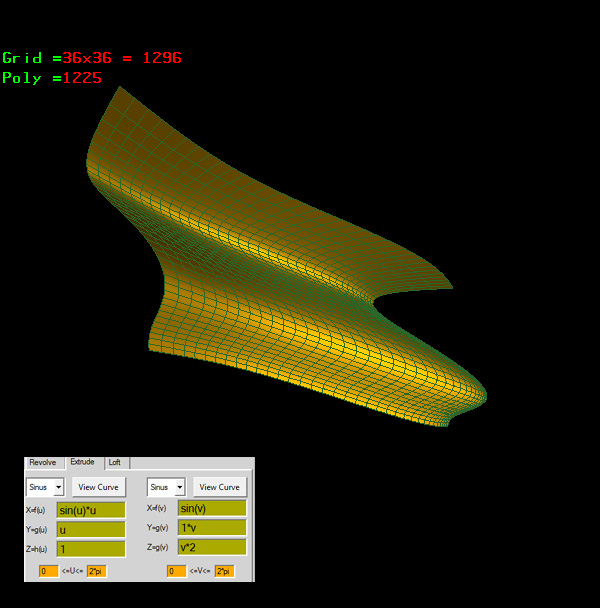
sinus
X=f(u) =sin(u)
Y=g(u) =cos(u)
Z=h(u) =-cos(u)
0<=u<=4*pi
cosinus
X=f(v) =sin(v)
Y=g(v) =cos(v)
Z=h(v) =v
0<=u<=4*pi





 rotacija oko z ose
rotacija oko z ose
 translacija po z-osi?
translacija po z-osi?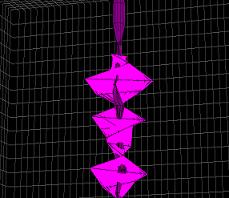
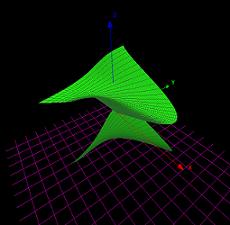































































































































































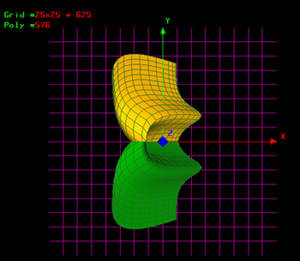
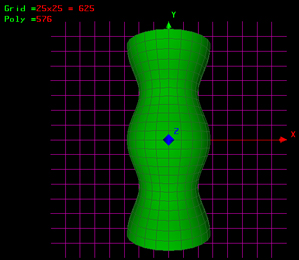
 1.
1. 2.
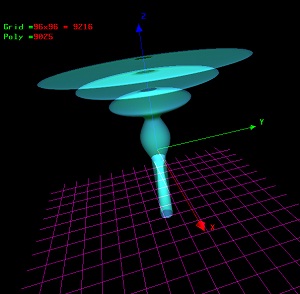
2.
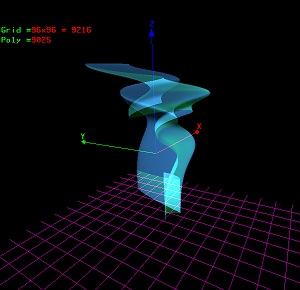
























 " />
" />