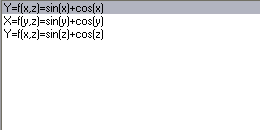
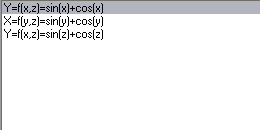
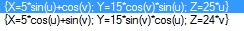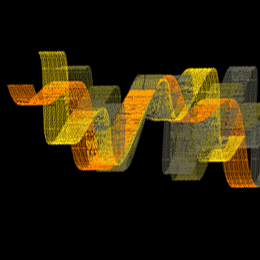MAT 03 - Površ u prostoru
3D Grapher
3D Math Explorer
Function Grapher
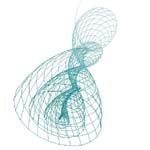
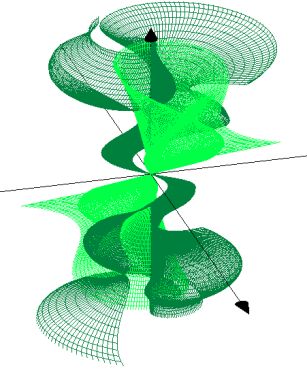
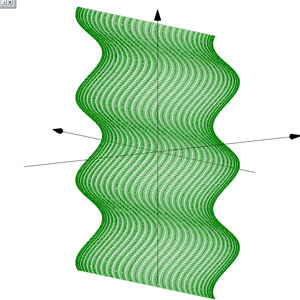
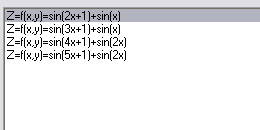
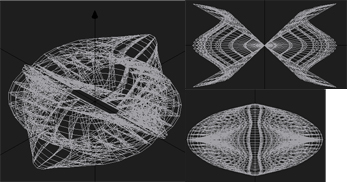
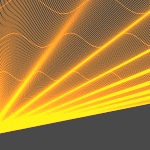
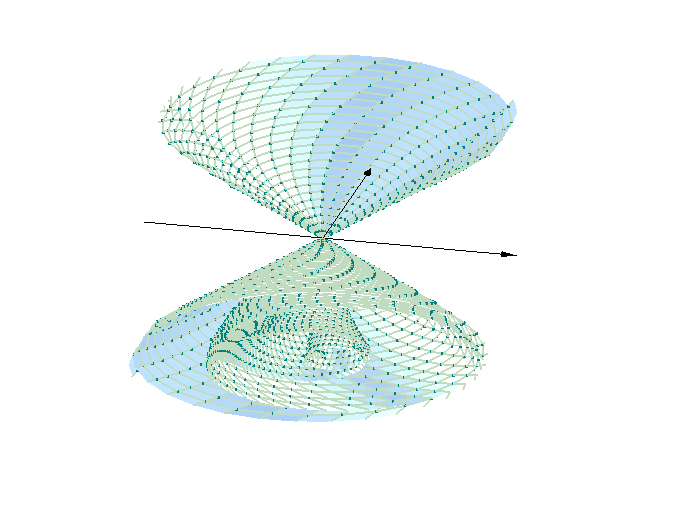
parametarski definisati i prikazati grafički izabranu površ u prostoru (jednu ili više). U tekstu dati parametarski oblik svih površi koje se nalaze na slici, kao i granice u i v.

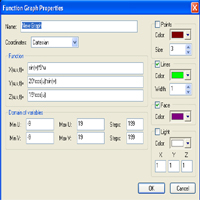
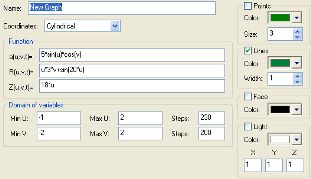
1. a=4*sin(u)*cos(v)
R=u*5*v
Z=16*u
Min U:-3; Max U:3
Min V:-3; Max V:3
steps 200
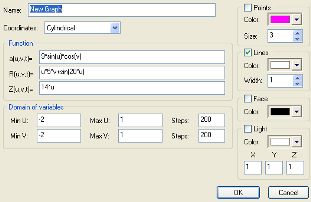
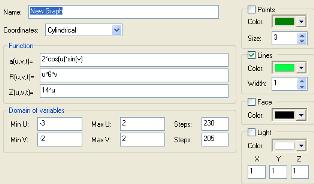
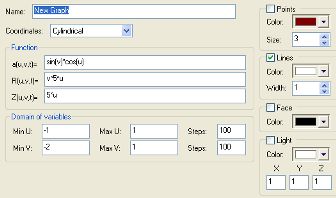
2. a=sin(v)*cos(u)
R=v*5*u
Z=5*u
Min U:-1; Max U:1
Min V:-1; Max V:1
steps 100
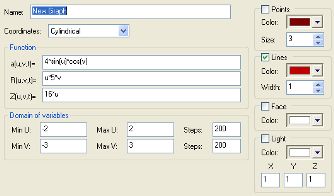
a=4*cos(u)*sin(v)
R=u*5*v
Z=16*u
MinU=-3 MaxU=3 Steps=200
MinV=-3 MaxV=3 Steps=200
a=10*sin(u)*cos(v)
R=u*5*v+sin(20*u)
Z=15*u
MinU=-2 MaxU=1 Steps=200
MinV=-2 MaxV=1 Steps=200

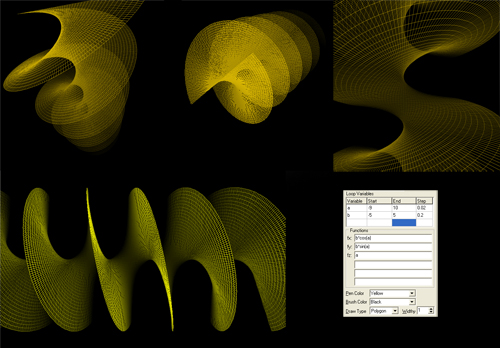
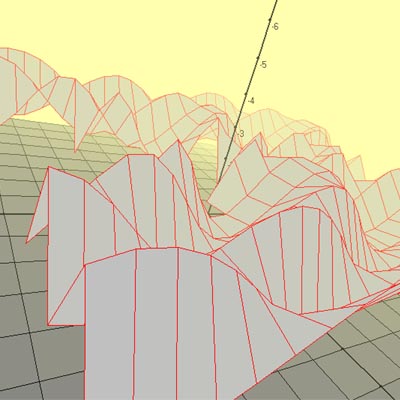
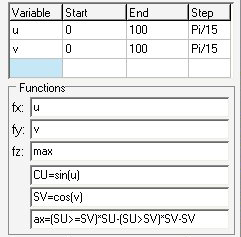
v; 0; 100; pi/15;
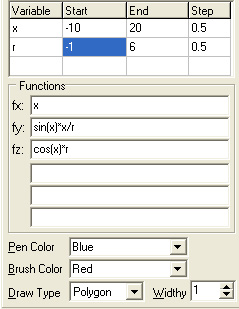
fx=u
fy=v
fz=max
SU=sin(u)
SV=cos(v)
max=(SU>=SV)*SU - (SU>SV)*SV

3D Grapher
X=sin(2*u)+cos(v); Y=sin(2*u)*v; Z=v
Umin = 0; U max = 4; vmin = 0, Vmax = 4
X=sin(2*u)+cos(v); Y=sin(2*u)*v; Z=v
Umin = -4; U max =0; vmin = -4, Vmax = 0
X=sin(2*u)+cos(v); Y=sin(2*u)*v; Z=v
Umin = 0; U max = 8 vmin = 0, Vmax = 8
X=sin(2*u)+cos(v); Y=sin(2*u)*v; Z=v
Umin = -8; U max =0; vmin = -8, Vmax = 0
X=sin(2*u)+cos(v)+1; Y=sin(2*u)*v+1; Z=v
Umin = 0; U max = 4; vmin = 0, Vmax = 4
X=sin(2*u)+cos(v)+1; Y=sin(2*u)*v+1; Z=v
Umin = -4; U max = 0; vmin = -4, Vmax = 0
X=sin(2*u)+cos(v)-1; Y=sin(2*u)*v-1; Z=v
Umin =0; U max = 4; vmin = 0, Vmax = 4
X=sin(2*u)+cos(v)-1; Y=sin(2*u)*v-1; Z=v
Umin = -4; U max = 0 ; vmin = -4, Vmax = 0
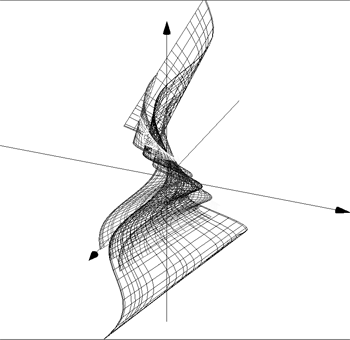
a(u,v,t)= 2*cos(v)*sin(v), R(u,v,t)=sin(v)+u, Z(u,v,t)=4*v
Min U=-10, Max U=10, Steps=100
Min V-10, Max V=10, Steps=100;
a(u,v,t)= 4*cos(v)*sin(v), R(u,v,t)=sin(v)+u, Z(u,v,t)=4*v
Min U=-5, Max U=5, Steps=100
Min V-5, Max V=5, Steps=100;
a(u,v,t)= 6*cos(v)*sin(v), R(u,v,t)=sin(v)+u, Z(u,v,t)=4*v
Min U=-3, Max U=3, Steps=100
Min V-3, Max V=3, Steps=100;
coordinates: cartesian
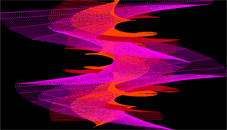
b: start o, end 2*pi, step pi/100
fx:R*cos(b)
fy:R*sin(a)*sin(a)
fz:R*cos(a)
R=cos(13*a)*sin(20*b)+10
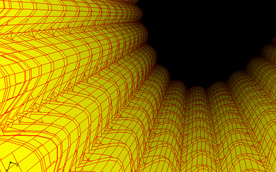
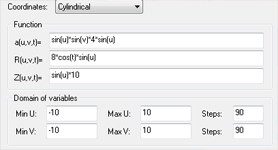
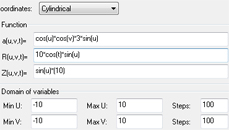
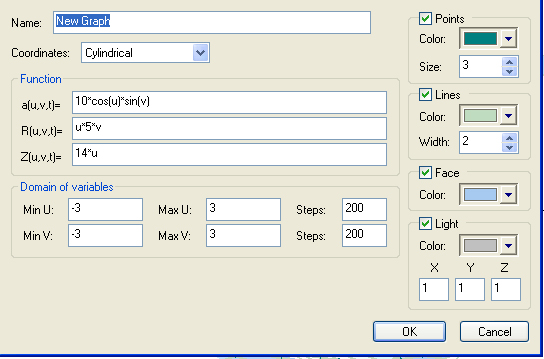
Cylindrical
a=u
R=2*v
Z=sin(7*v-t)/(1+v)^2
Min u=0 Max u=6.2832 Steps 60
Min v=0 Max v=4 Steps 60
I
x=sin(2*u)+cos(v)
y=sin(2*u)*v
z=u
minU=-10, maxU=10 steps 40
minV=-15, maxV=15 steps 40
II
x=sin(2*u)+cos(v)+1
y=sin(2*u)*v+1
z=v
minU=-5, maxU=5 steps 40
minV=-40, maxV=40 steps 40
III
x=sin(2*u)+cos(v)+3
y=sin(2*u)*v
z=v
minU=-10, maxU=10 steps 40
minV=-5, maxV=5 steps 40

U: -3,3; 400
V: -3,3; 400
X:2*sin(u)*4*cos(v); Y:4*cos(u); Z:16*cos(v)
U:-5,5; 300
V: -5,5; 300
X:6*cos(v)*cos(u); Y:3*sin(v); Z:cos(u)*2*cos(u)
U: -5,5; 100
V: -5,5; 100
X:sin(u)*8*sin(v); Y:3*cos(u); Z:sin(u)
U: -3,3; 100
V: -3,3; 100
3D Grapher

3D Grapher
- Cylindrical
a=5*cos(v)*sin(u)
R=v*5*u
Z=16*u
minu=-8 maxu=8 steps 500
minv=-8 maxv=8 steps 500
- Cylindrical
a= cos(u)*sin(v)
R= 5*u*v+sin(15*v)
Z= 15*v
minu=-10 maxu=10 steps 300
minv=-10 maxv=10 steps 500
- Cartesian
X= 10*sin(u)*cos(v)
Y= u*5*v+sin(10*u)
Z=15*v
minu=-2 maxu=2 steps 200
minv=-2 max=2 steps 200

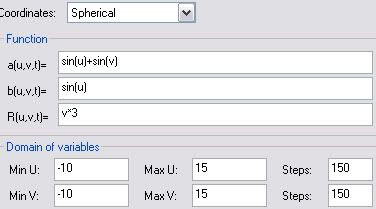
a=sin(u)+sin(v) r=cos(v)-2 z=cos(v)
min u=-10 max u=-6; min v=-10 max v=-6; steps 20
a=sin(u)+sin(v) r=cos(v)+2 z=cos(v)
min u=-10 max u=-6; min v=-10 max v=-6; steps 20
a=sin(u)+sin(v) r=cos(v)-4 z=cos(v)
min u=-10 max u=-6; min v=-10 max v=-6; steps 20
a=sin(u)+sin(v) r=cos(v)+4 z=cos(v)
min u=-10 max u=-6; min v=-10 max v=-6; steps 20
a=sin(u)+sin(v) r=cos(v)-6 z=cos(v)
min u=-10 max u=-6; min v=-10 max v=-6; steps 20
a=sin(u)+sin(v) r=cos(v)+6 z=cos(v)
min u=-10 max u=-6; min v=-10 max v=-6; steps 20

3D Grapher
x=8*sin(u)*cos(v)
y=8*sin(u)*cos(v)
z=18*u
U=(5,3), V=(5,3), steps= 100
x=3*sin(u)*cos(v)
y=9*v*u-sin(15*u)
z=50*u
U=(5,3), V=(5,3), steps= 100
Y= u*4*v
Z= 13*u
Mmin U= -5 maxU= 5 steps= 200
Mmin U=-5 maxU= 5 steps= 200
X=10*sin(u)*cos(v)
Y= u*5*v+sin(20*u)
Z= 15*u
Mmin U= -6 maxU= 6 steps= 150
Mmin U=-3 maxU= 3 steps= 150
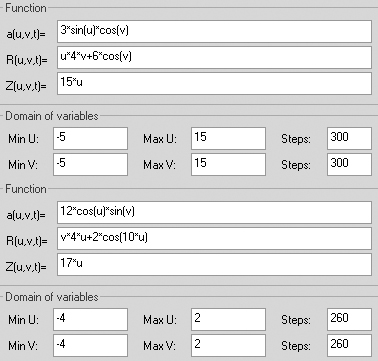
X=4*sin(u)+cos(v)
Y=u*3*v+sin(20*u)
Z= 12*u
Mmin U= -3 maxU= 6 steps= 200
Mmin U=-3 maxU= 6 steps= 200

name:1
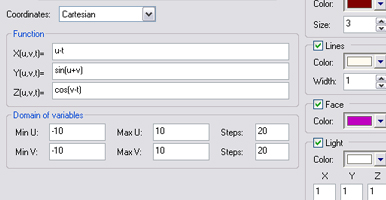
coordinates: Cartesian
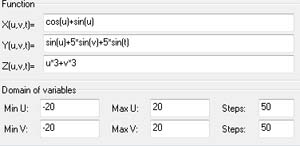
Function:
X(u,v,t)=u+u+v+t
Y(u,v,t)=v+u+u+u+u+u+u+u+u+u+u+u+u
Z(u,v,t)=t+t+sin(t)+v+u+u+u+u+cos(u+u)
Min U=-10 Max U=10 Steps 20
Min V=-10 Max V=10 Steps 20
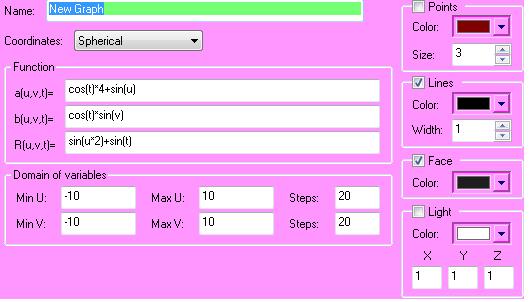
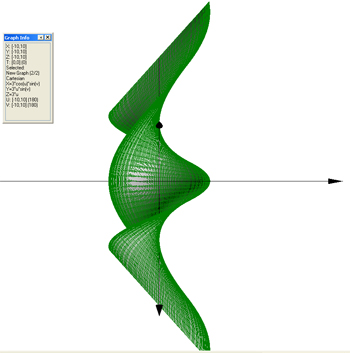
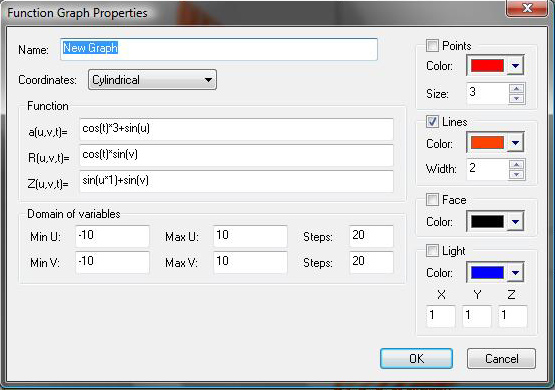
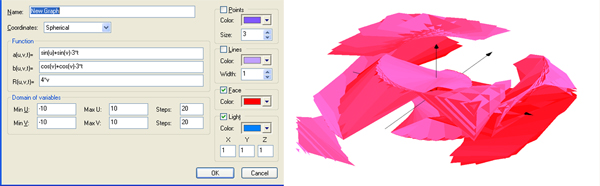
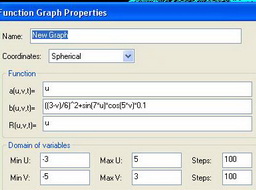
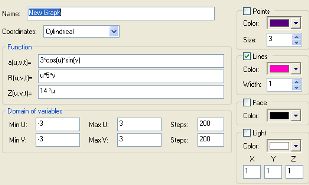
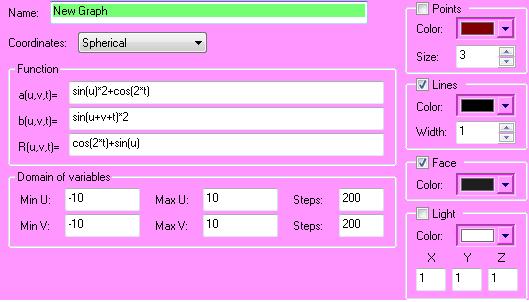
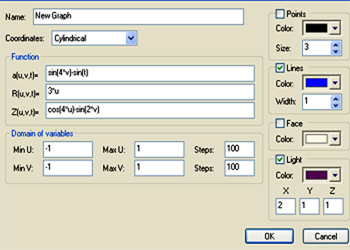
Name: New Graph
coordinates: Cartesian
Function:
X(u,v,t)=cos(u)+sin(v+t)-cos(u+u)
Y(u,v,t)=sin(v)
Z(u,v,t)=cos(t)+t+u+v+sin(v+t)
Min U=-10 Max U=10 Steps 20
Min V=-10 Max V=10 Steps 20
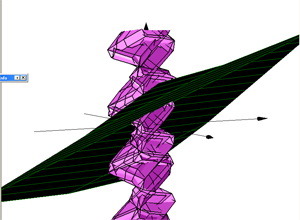
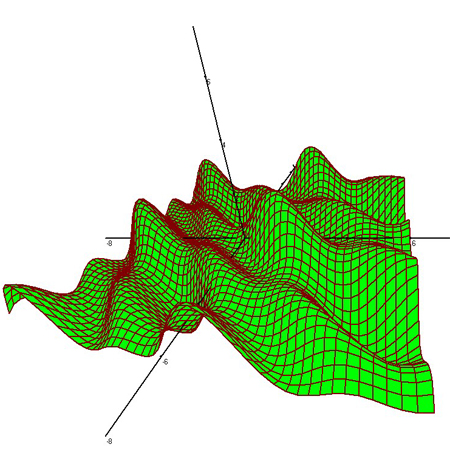
f(x)=x
f(y)=y
f(z)=1/(x*x+1) - 2/(y*y+1) - 0.5*sin(5*r)/r
r=-(x*x+y*y)^0.5
Druga f-ja: x,y od -5 do 5 ; step=0.25
f(x)=x
f(y)=y
f(z)=-1/(x*x+1) + 2/(y*y+1) + 0.5*sin(5*r)/r
r=+(x*x+y*y)^0.5

1. a=5*cos(v)*sin(u)
r=v*5*u
z=13*u
minu=-10 maxu=10 steps 500
minv=-10 maxv=10 steps 500
2. a=cos(u)*sin(v)
r=5*u*v+sin(15*v)
15*v
minu=-10 maxu=10 steps 200
minv=-10 maxv=1- steps 200
3.x=5*sin(v)*cos(u)
y=5*u*t
z=15*v
minu=-10 maxu=10 steps 20
minv=-10 max=10 steps 20
4. x=10*sin(u)*cos(v)
y=u*5*v+sin(10*u)
z=13*u
minu=-3 maxu=1 steps 200
minv=-3 maxv=1 steps 200

y=u*v
z=cos(u+v)-v
minU:-5; maxu:5; steps:120
minv:-5; maxv:5; steps 120
2. a=sin(v*u)-cos(u)*u*2
b=5*v
R=5*u*v
minu:-5; maxu:5; steps 150
minv:-5; maxv:5; steps 150
3. x=cos(u*2)+sin(v*3)
y=2*sin(u)
z=3*cos(v)
minu:-10; maxu:10; steps:100
minv:-10; maxv:10; steps:100
3d grapher

1)cylindrical
a=1*u
R=20*sin(u)*cos(v)
Z=u*5*v+sin(15*u)
minU=-3; maxU=3; steps=200
minV=-3; maxU=3; steps=200
2)cylindrical
a=u*2*v
R=20*u
Z=20*cos(u)*sin(v)
minU=-3; maxU=3; steps=200
minV=-3; maxU=3; steps=200
3)cylindrical
a=1*sin(u)*cos(v)
R=u*15*v+sin(5*u)
Z=5*u
minU=-3; maxU=3; steps=200
minV=-3; maxU=3; steps=200
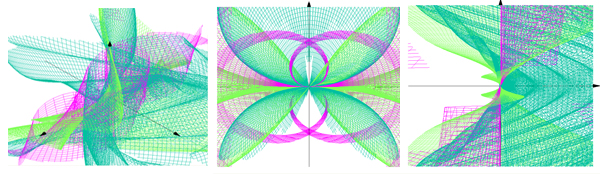
3d grapher
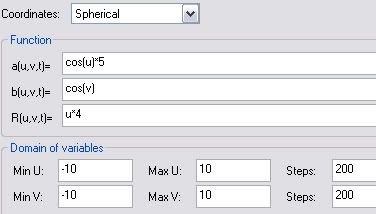
coordinates:spherical
a=cos(v)+1
b=cos(u)*sin(u)+1
c=cos(v)*cos(u)+1
domain of variables:
min u =-5 max u=5 steps 200
min v=-10 max v=10 steps 200
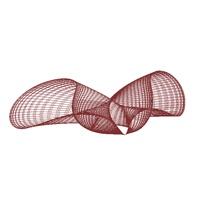
3D Grapher
1. 2.
coordinates:cartesian coordinates:cartesian
function function
X(u,v,t)=10*sin(u)*cos(v) X(u,v,t)=15*sin(u)*cos(v)
Y(u,v,t)=u*5*v+sin(20*u) Y(u,v,t)=u*5*v+sin(20*u)
Z(u,v,t)=35*u Z(u,v,t)=30*u
domain of variables: domain of variables:
min U: -5 max U:1 steps: 250 min U: -10 max U:1 steps:230
min V: -5 max V: 1 steps: 250 min V: -10 max V:1 steps:230
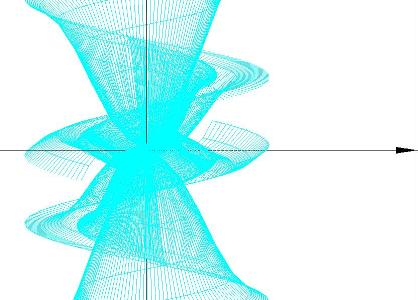
f(x)=sin(20*x)
f(y)=sin(20*x)*cos(20*x)
f(z)=cos(20*x)
PS
Tek danas sam shvatio da slika koju sam postavio kao odgovor na drugi zadatak u stvari apsolutno nije adekvatna za njega, već odgovara ovoj temi, pa evo limka i do nje. Link
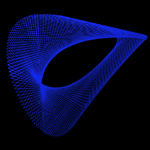
3D Grapher
Coordinates: Cylindrical
a= 3*sin(v)
R= 4*cos(60)*sin(u)+cos(u)
Z= u
Min U: -10 Max U: 10 Steps: 10
Min V: -10 Max V: 10 Steps: 20

a=u^2+v^2 u (-1, 1) steps: 20
R=3*v^2 v(-1, 1) steps: 90
Z=4*u^2
II funkcija> Cylindrical
a=2*u^2+v^2 u (-1, 1) steps: 20
R=4.5*v^2 v (-1, 1) steps: 90
Z=5.5*u^2
II funkcija> Cylindrical
a=4*u^2 u(-1, 1) steps: 56
R=u^2+v^2 v(-1, 1) steps:120
Z=3*v^2
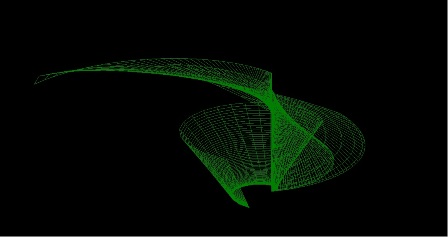
cylindrical
a=13*sin(t)*sin(v)
R=v*10*u+sin(15*t)
Z=10*v
min U=-5 max U=20 steps=200
min U=-5 max U=20 steps=200
cartesian
a=10*sin(t)*sin(v)
R=v*17*u+sin(12*t)
Z=10*v
min U=-4 max U=3 steps=300
min U=-4 max U=3 steps=300
nadam se da je dobro :)

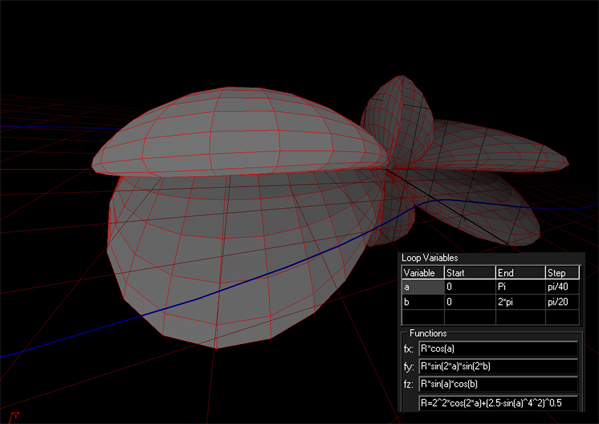
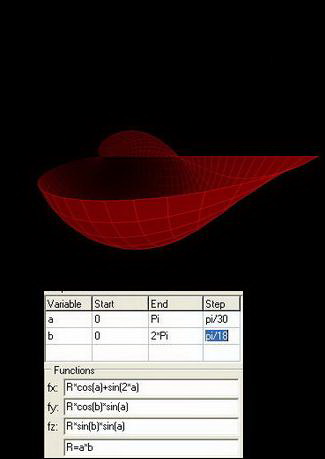
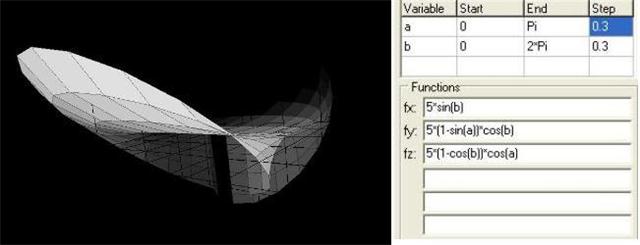
Povrs 1
a ; 0 ; Pi ; pi/80
b ; 0 ; 2*Pi ; pi/80
Fx: R*sin(a)*cos(b)
Fy: R*sin(a)*sin(b)
Fz: R*cos(a)
R=cos(20*a)*sin(15*b)+10
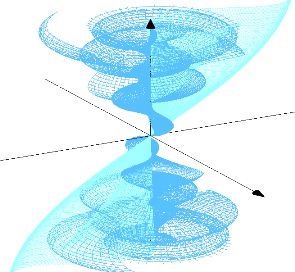
Povrs 2
t ; 0 ; Pi ; pi/20
b ; 0 ; 20 ; pi/20
Fx=R*cos(theta)
Fy=R*sin(theta)
Fz=3*b
theta=t+b*3
k=1
R=cos(t*k)*b
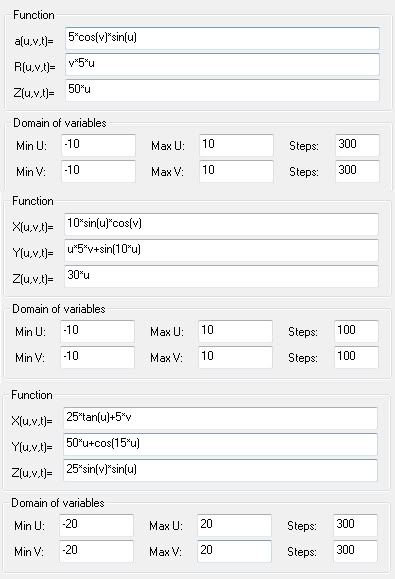
1. Cylindicar
a(u,v,t)=2*sin(v)*cos(u)
R(u,v,t)=v*u
Z(u,v,t)=5*u+t
U(-3; 5), Steps(100)
V(-4; 4), Steps(100)
2. Cartesian
X(u,v,t)=10*sin(u)*cos(v)
Y(u,v,t)=u*5*v+sin(10*u)
Z(u,v,t)=13*u
U(-10; 10), Steps(200)
V(-10; 10), Steps(200)
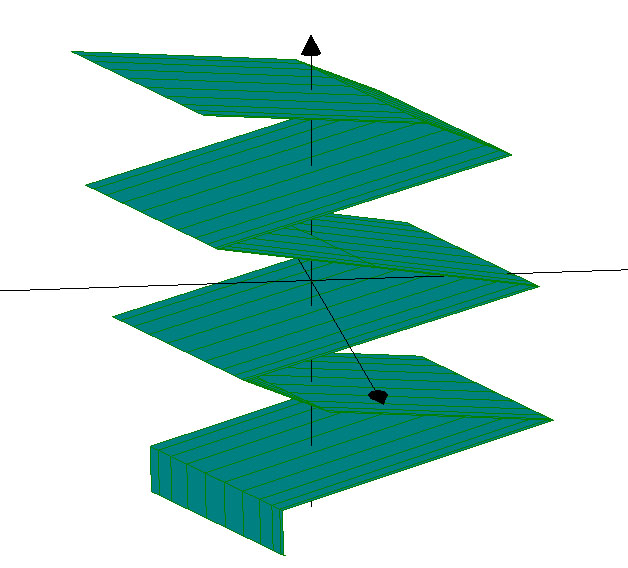
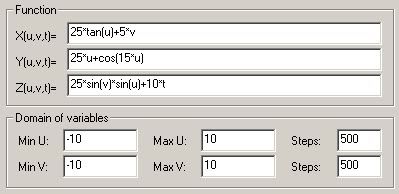
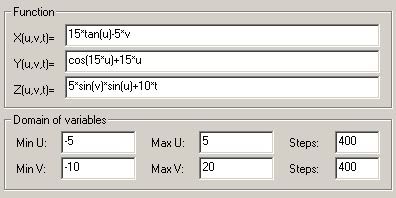
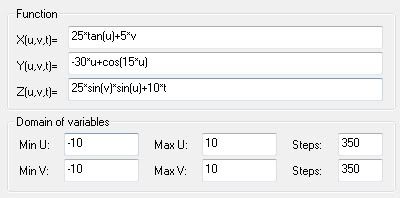
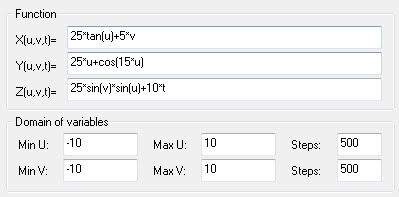
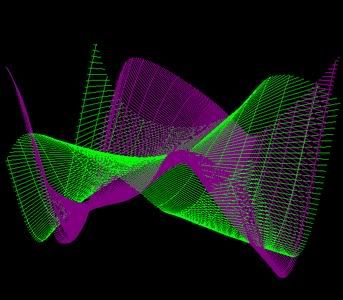
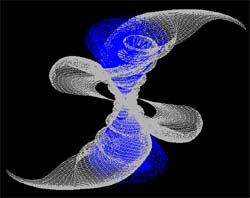
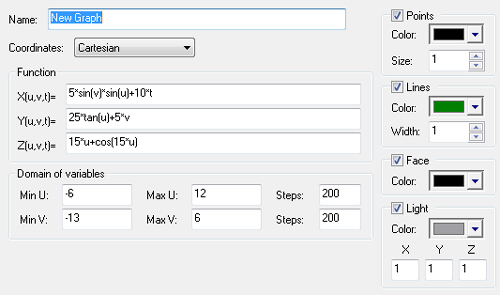
3. Cartesian
X(u,v,t)=25*tan(u)+5*v
Y(u,v,t)=25*u+cos(15*u)
Z(u,v,t)=25*sin(v)*sin(u)+10*t
U(-3; 1), Steps(100)
V(-3; 2), Steps(100)

a(u,v,t)= 16*cos(u)*sin(v)
R(u,v,t)= u*5*sin(v)
Z(u,v,t)= 8*u+v
max U: -10 max V: 19 steps 200
min U: -5 min V: 2 steps 100

1.
a=8*sin(u)*cos(v), R=5*v*u+sin(20*u), Z=18*u
Umin=-5, Umax=3, steps: 100
Vmin=-5, Vmax=3 steps:100
2.
a=3*sin(u)*cos(v), R=9*v*u-sin(15*u), Z=50*u
Umin=-5, Umax=3, steps: 100
Vmin=-5, Vmax=3 steps:100

3D Grapher
prva povrs druga povrs
coordinates:cartesian coordinates:cartesian
function function
X(u,v,t)=10*sin(u)*cos(v) X(u,v,t)=15*sin(u)*cos(v)
Y(u,v,t)=u*5*v+sin(20*u) Y(u,v,t)=u*5*v+sin(20*u)
Z(u,v,t)=35*u Z(u,v,t)=30*u
domain of variables: domain of variables:
min U: -5 max U:1 steps: 250 min U: -10 max U:1 steps:230
min V: -5 max V: 1 steps: 250 min V: -10 max V:1 steps:230
X=sin(2*u)+cos(v); Y=sin(2*u)*v; Z=v
Umin = 0; U max = 4; vmin = 0, Vmax = 4
X=sin(2*u)+cos(v); Y=sin(2*u)*v; Z=v
Umin = -4; U max =0; vmin = -4, Vmax = 0
X=sin(2*u)+cos(v); Y=sin(2*u)*v; Z=v
Umin = 0; U max = 8 vmin = 0, Vmax = 8
X=sin(2*u)+cos(v); Y=sin(2*u)*v; Z=v
Umin = -8; U max =0; vmin = -8, Vmax = 0
X=sin(2*u)+cos(v)+1; Y=sin(2*u)*v+1; Z=v
Umin = 0; U max = 4; vmin = 0, Vmax = 4
X=sin(2*u)+cos(v)+1; Y=sin(2*u)*v+1; Z=v
Umin = -4; U max = 0; vmin = -4, Vmax = 0
X=sin(2*u)+cos(v)-1; Y=sin(2*u)*v-1; Z=v
Umin =0; U max = 4; vmin = 0, Vmax = 4
X=sin(2*u)+cos(v)-1; Y=sin(2*u)*v-1; Z=v
Umin = -4; U max = 0 ; vmin = -4, Vmax = 0
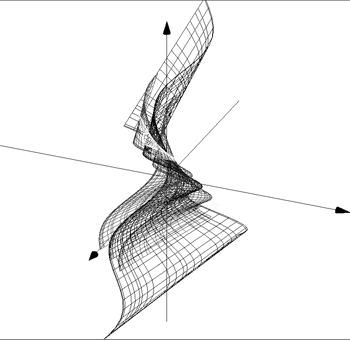
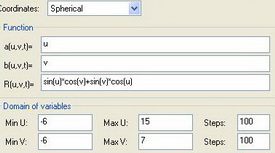
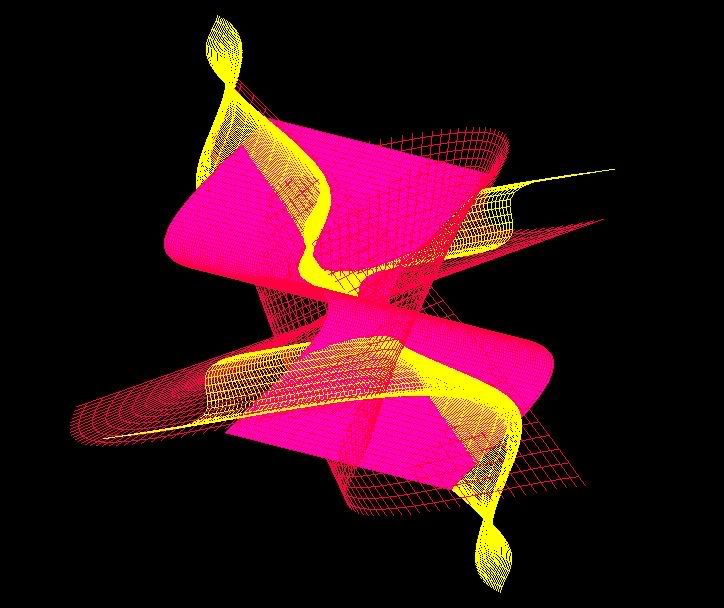
X=sin(u)*cos(cos(u))
Y=v*u*sin(v)
Z=cos(v)
Min U:-1 Max U:1 steps:100
Min V:-2 Max V:2 steps:100
X=sin(u)*cos(cos(u))
Y=v*u*sin(v)
Z=sin(v)
Min U:-1 Max U:1 steps:100
Min V:-2 Max V:2 steps:100
X=sin(u)*cos(cos(u))
Y=v*u*sin(v)*sin(v)*0.3
Z=cos(v)*0.3
Min U:-1 Max U:1 steps:100
Min V:-2 Max V:2 steps:100

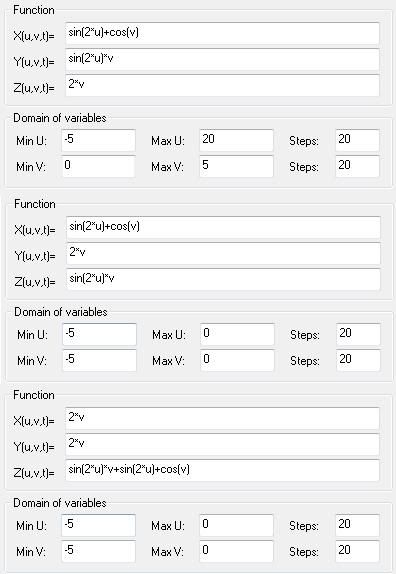
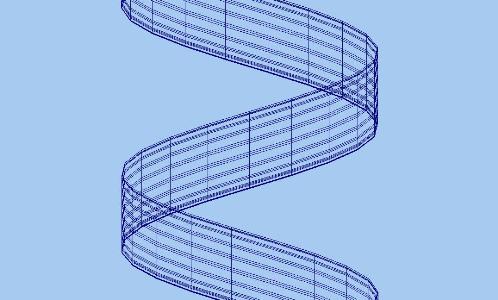
y=sin(2*u)*v
z=2*v
min U=-5 max U=20 steps=20
min V=0 max V=5 steps=20
x=sin(2*u)+cos(v)
y=2*v
z=sin(2*u)*v
min U=-5 max U=15 steps=20
min V=-5 max V=15 steps=20
x=2*v
y=2*v
z=sin(2*u)*v+sin(2*u)+cos(v)
min U=-5 max U=0 steps=20
min V=-5 max V=0 steps=20
x=v
y=sin(2*u)+cos(v)*3
z=sin(2*u)*v
min U=0 max U=6 steps=20
min V=0 max V=10 steps=20
x=2*v
y=-2*v
z=sin(2*u)*v+sin(2*u)+cos(v)
min U=-5 max U=0 steps=20
min V=-5 max V=0 steps=20

3D Grapher- Cylindrical
2*cos(u)*cos(v)
2*sin(v)
v
-10 10 200; -10 10 200

Cylindrical
a=10*sin(v)*cos(u), r=5*u*v, z=6*v
Cylindrical
x=10*sin(v)*cos(v), y=10*u*v, z=10*u
Cylindrical
a=2*sin(v)*cos(u), r=v*u, z=5*u+t
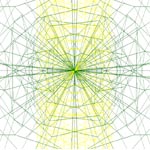
X=cos(3*v)+sin(u); Y=cos(3*v)*u; Z=u
Umin = 0; U max = 5; vmin = 0, Vmax = 5
X=cos(3*v)+sin(u); Y=cos(3*v)*u; Z=u
Umin = -5; U max =0; vmin = -5, Vmax = 0
X=cos(3*v)+sin(u); Y=cos(3*v)*u; Z=u
Umin = 0; U max = 10 vmin = 0, Vmax = 10
X=cos(3*v)+sin(u); Y=cos(3*v)*u; Z=u
Umin = -10; U max =0; vmin = -10, Vmax = 0
X=cos(3*v)+sin(u)+1; Y=cos(3*v)*u+1; Z=u
Umin = 0; U max = 5; vmin = 0, Vmax = 5
X=cos(3*v)+sin(u)-1; Y=cos(3*v)*u-1; Z=u
Umin = -5; U max = 0; vmin = -5, Vmax = 0
X=cos(3*v)+sin(u)+1; Y=cos(3*v)*u-1; Z=u
Umin =0; U max = 10; vmin = 0, Vmax = 10
X=cos(3*v)+sin(u)+1; Y=cos(3*v)*u-1; Z=u
Umin = -10; U max = 0 ; vmin = -10, Vmax = 0