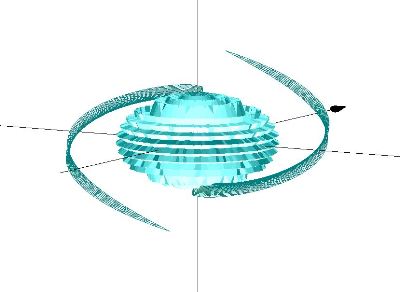
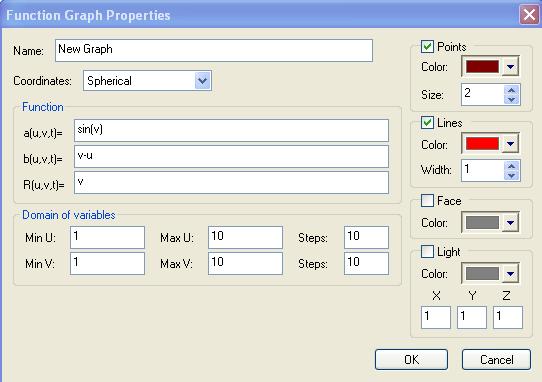
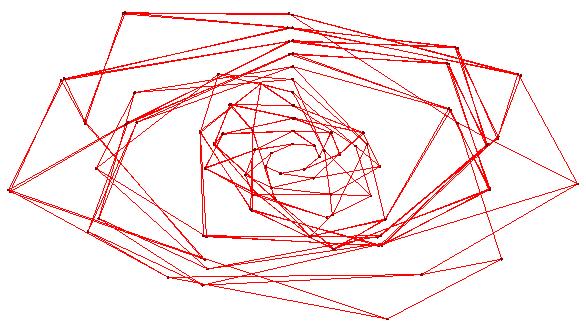
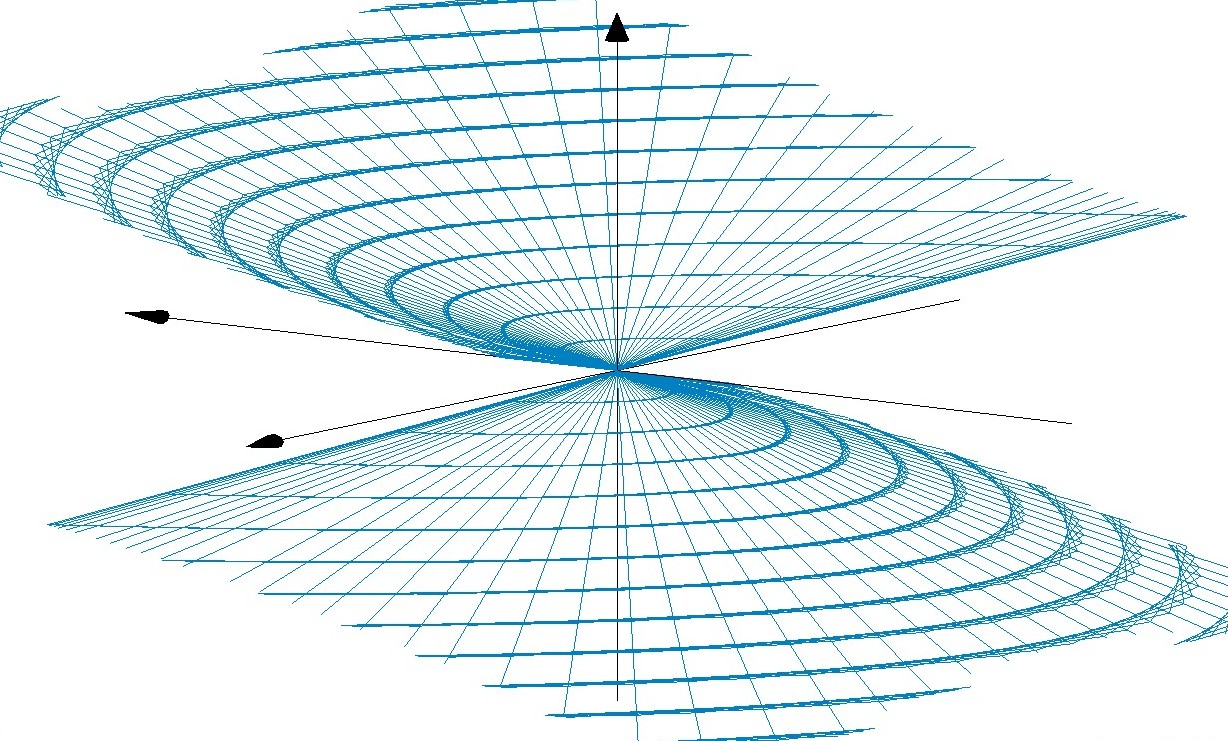
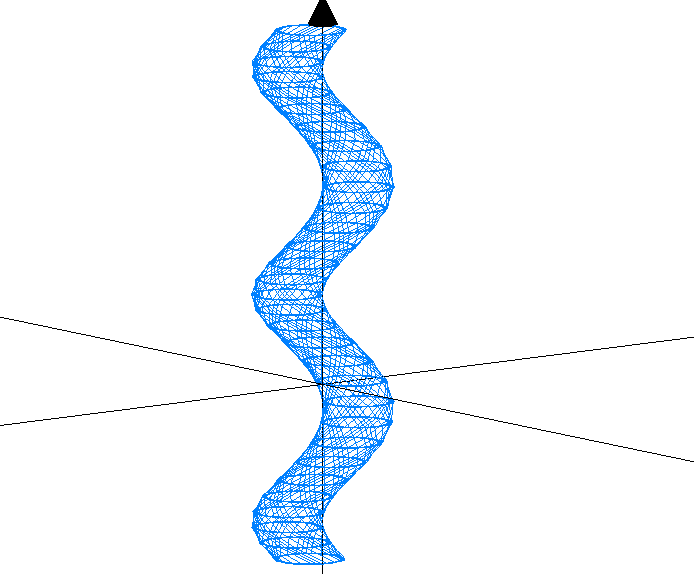
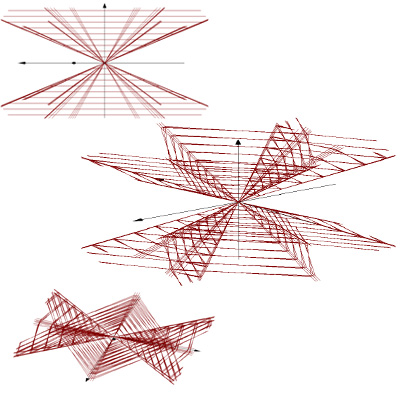
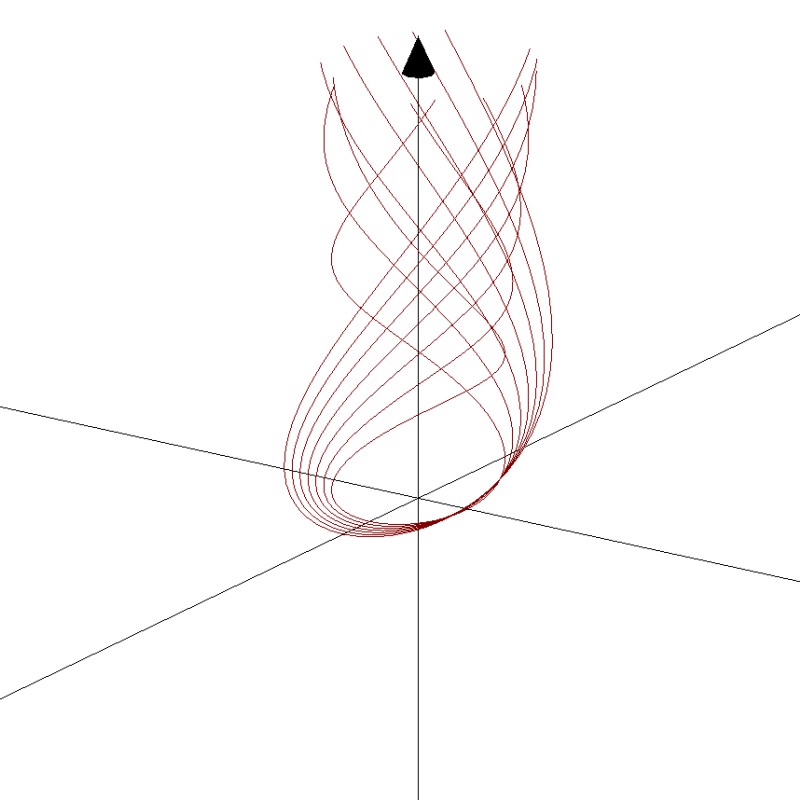
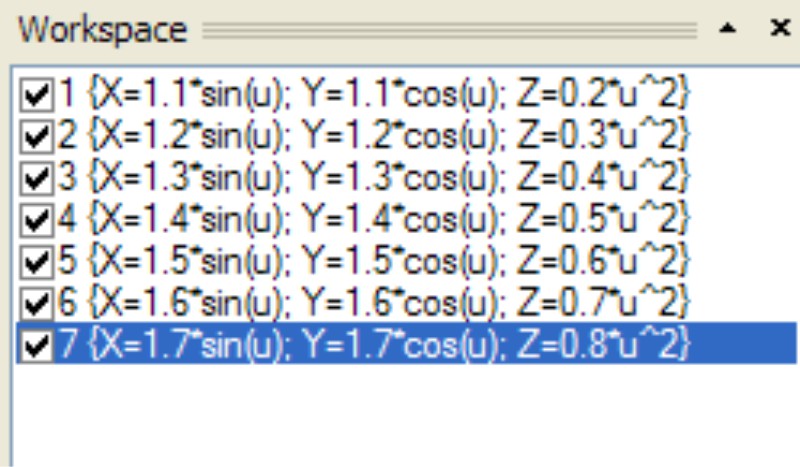
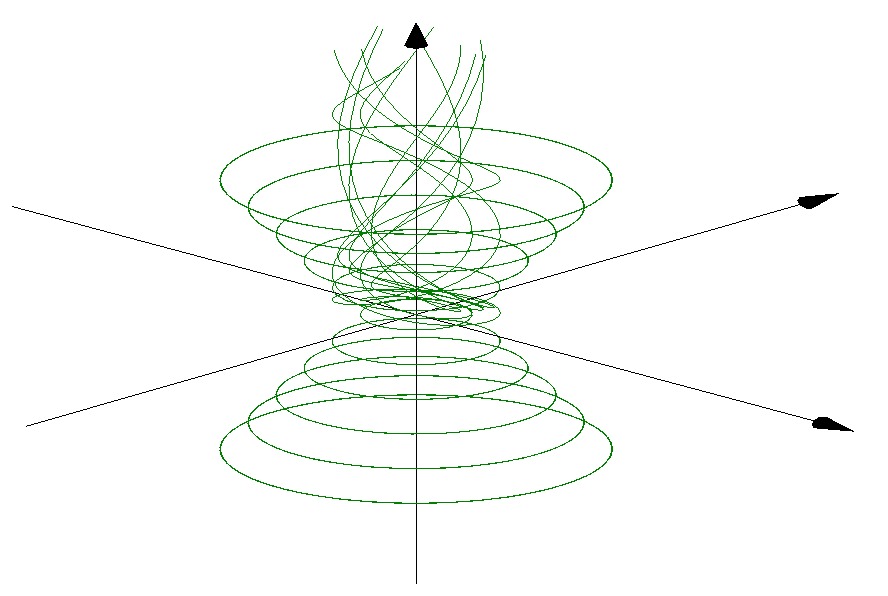
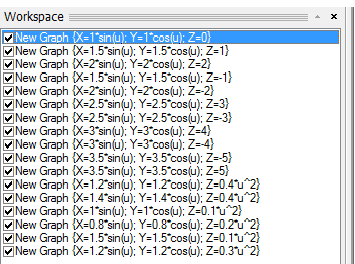
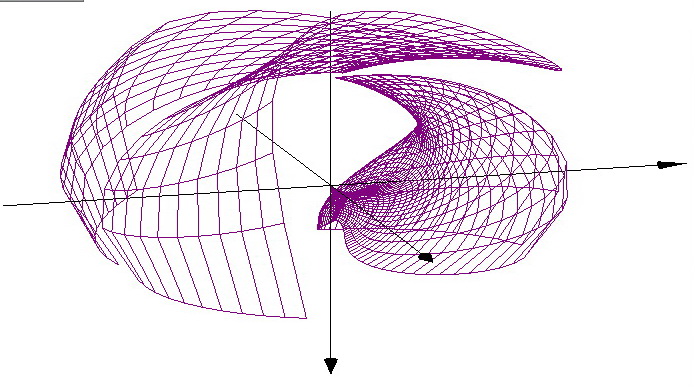
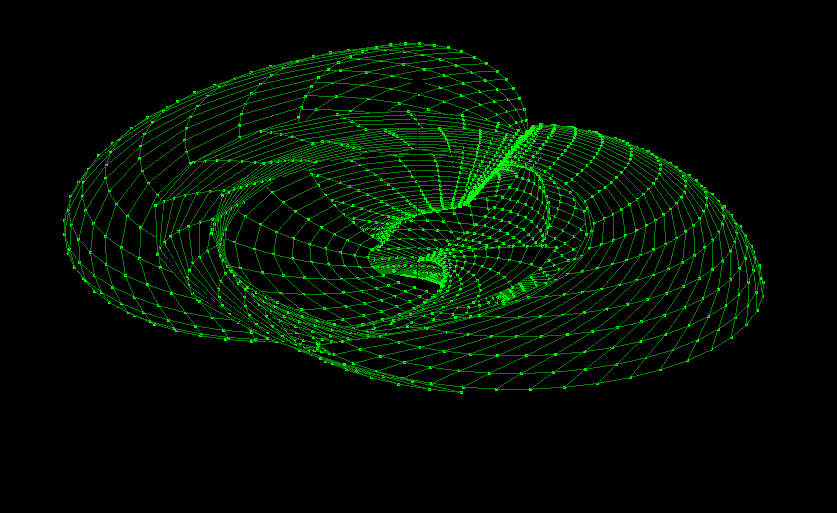
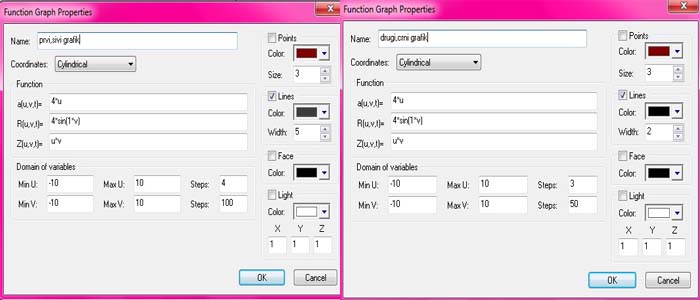
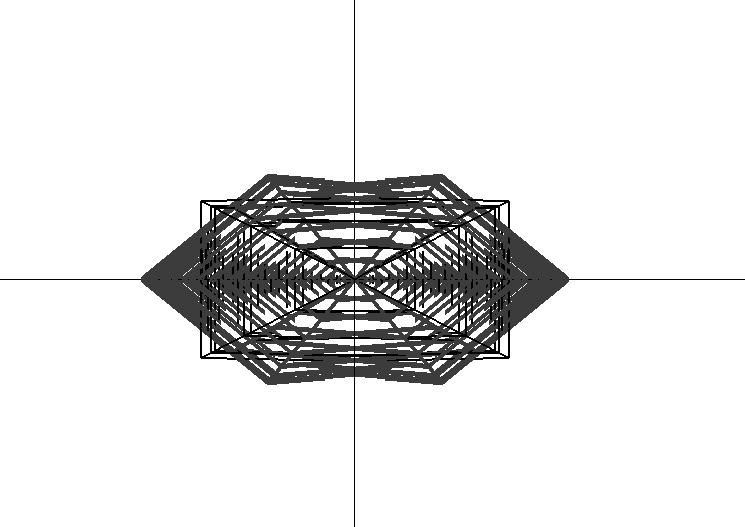
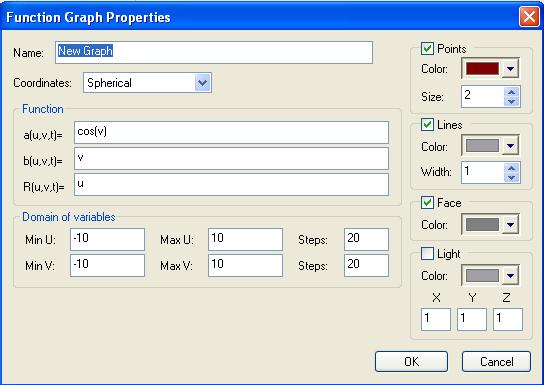
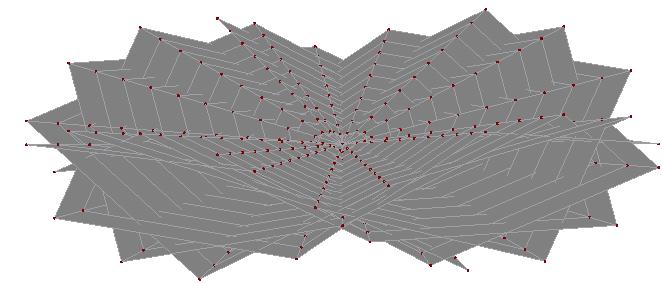
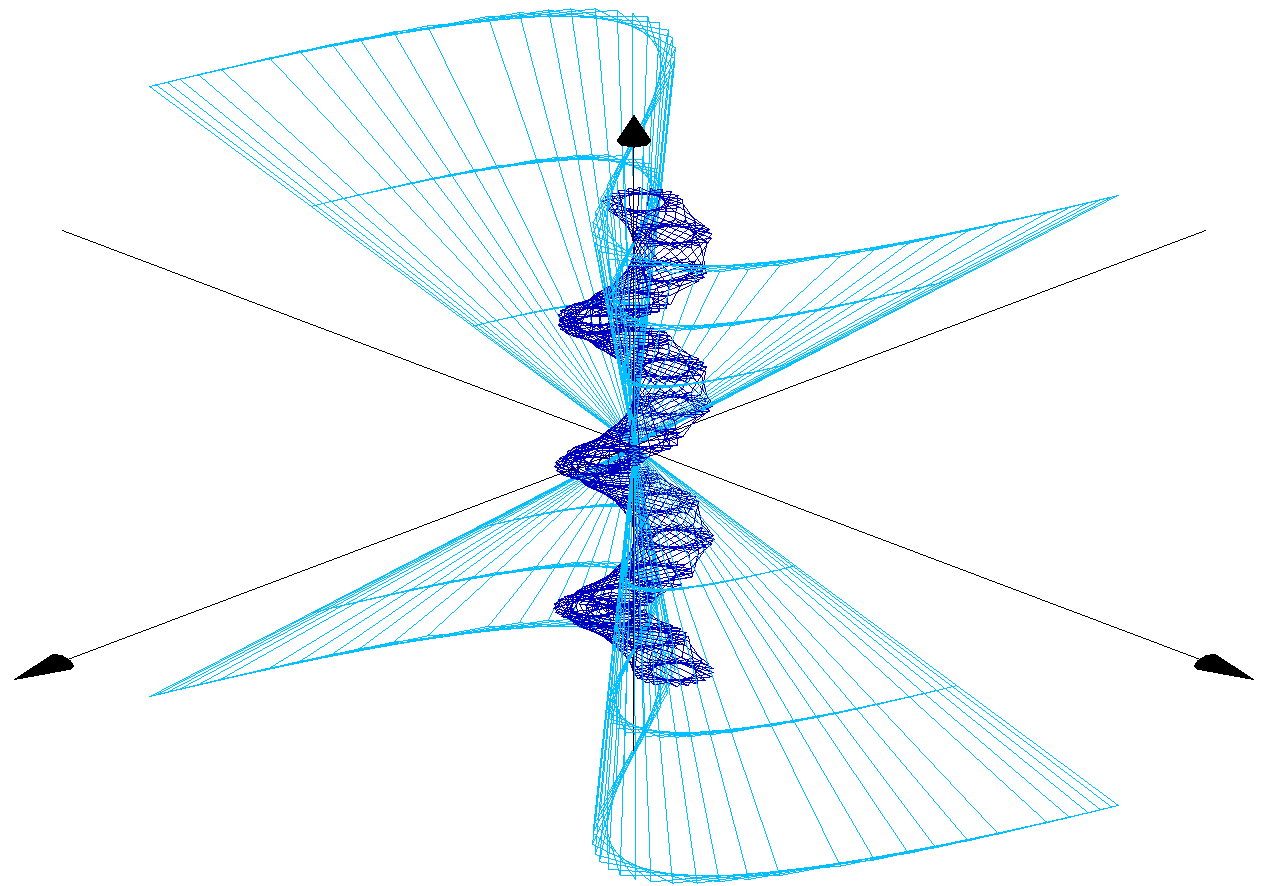
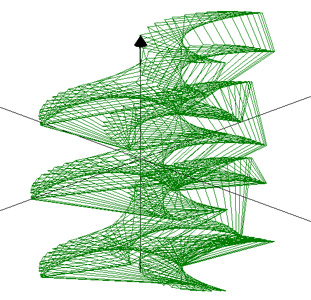
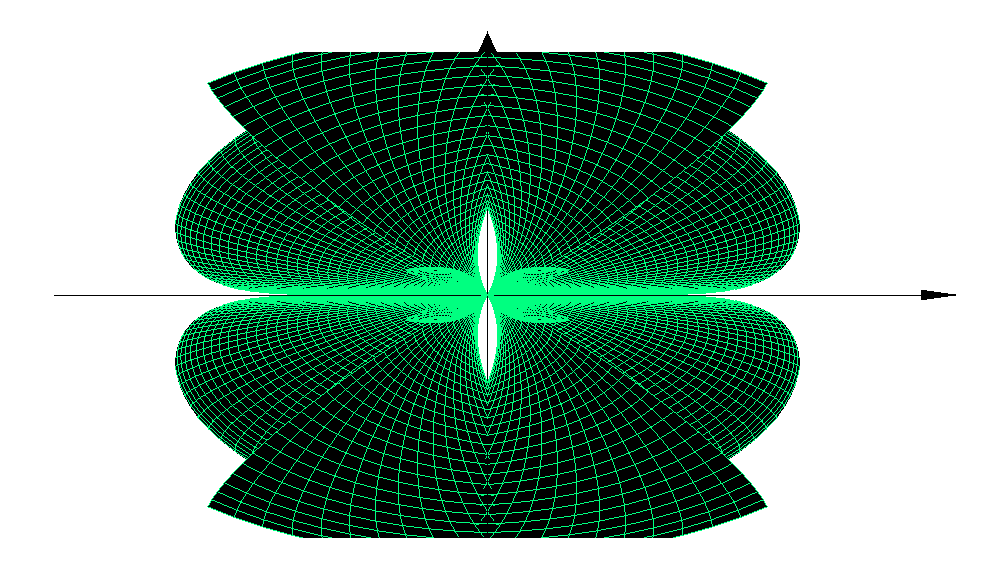
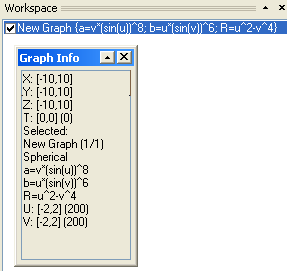
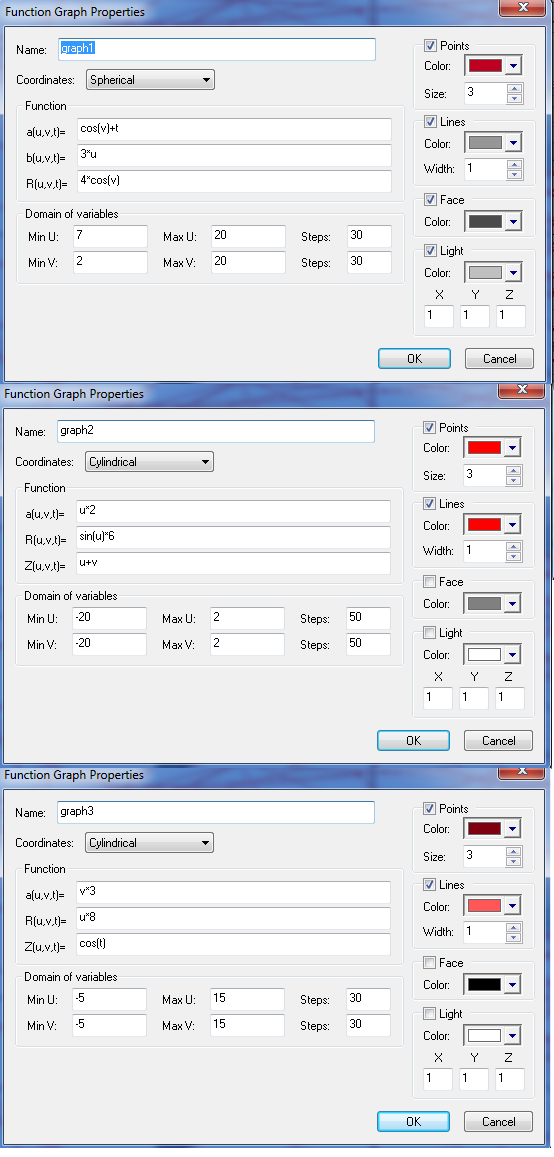
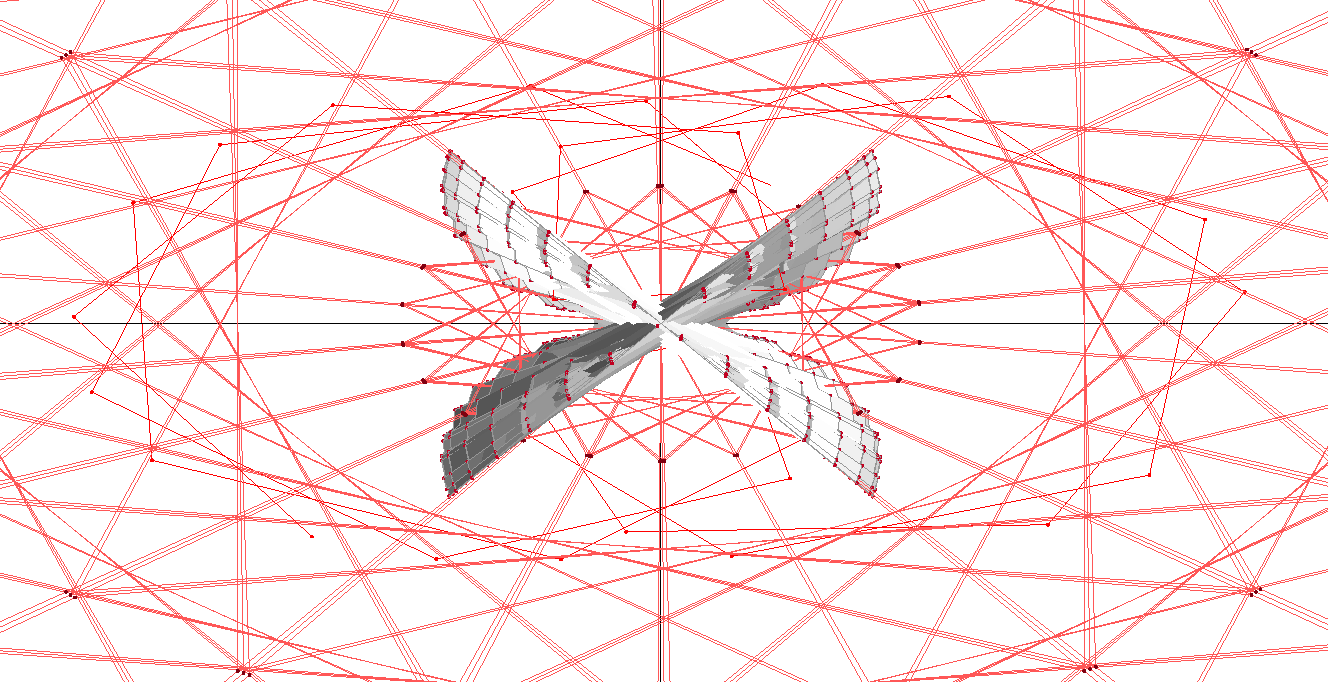
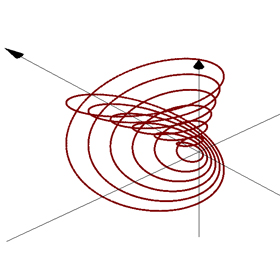
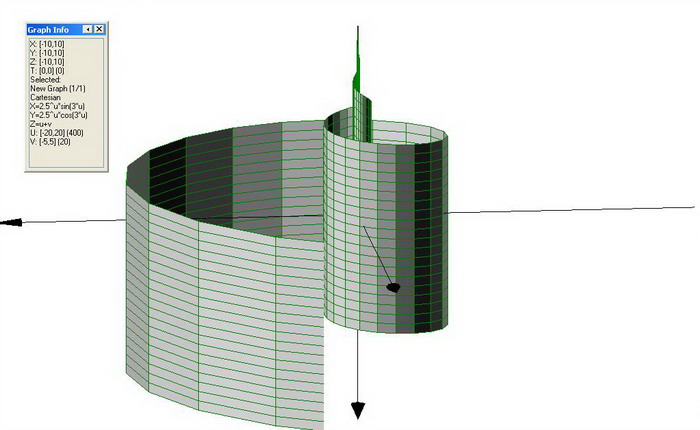
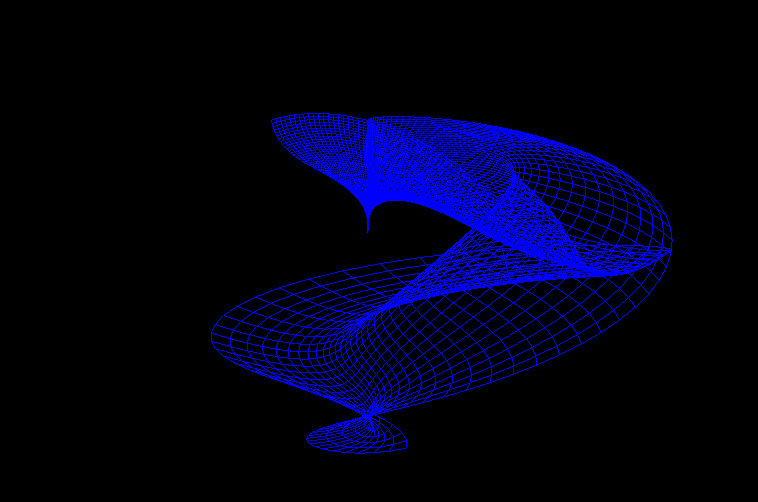
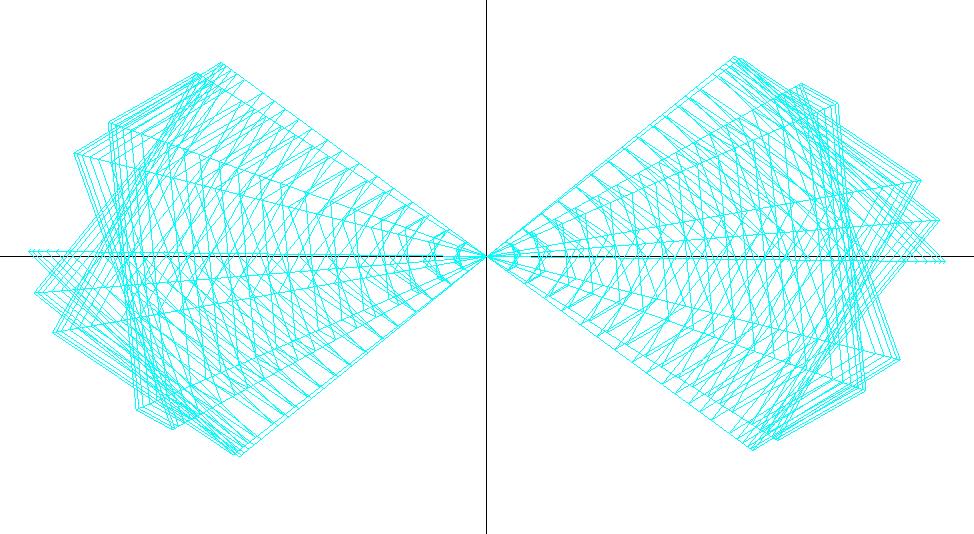
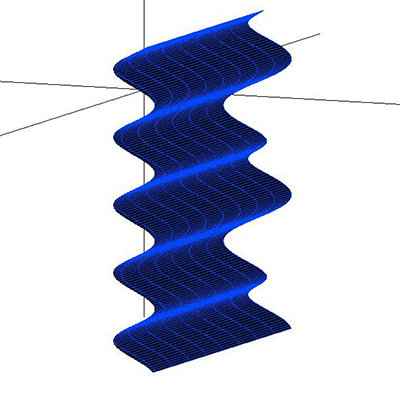
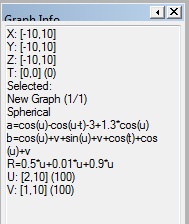
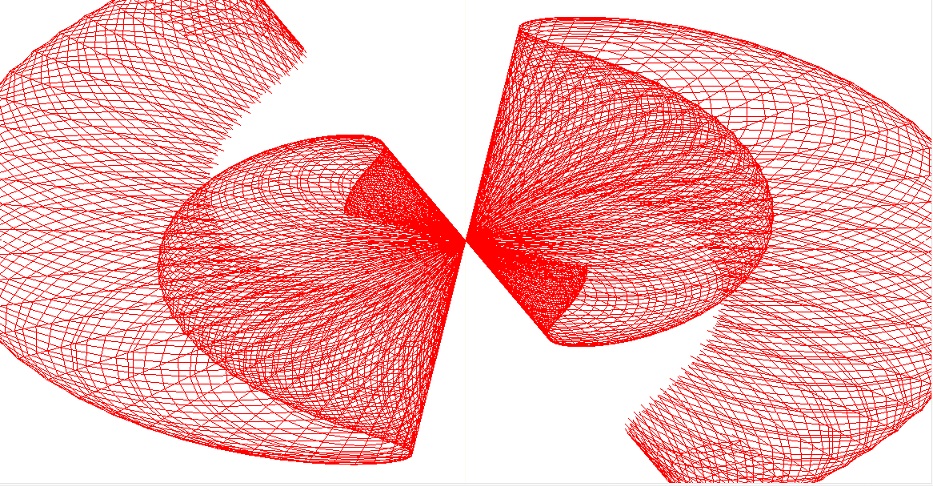
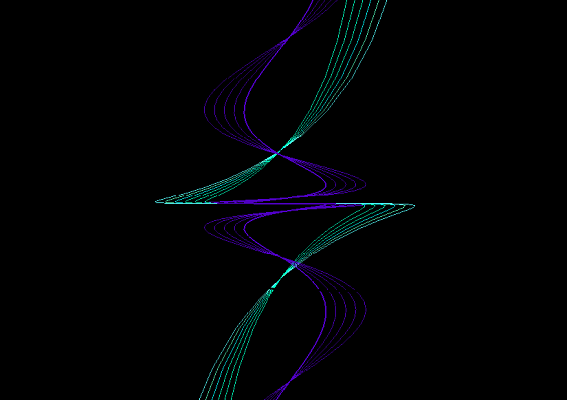
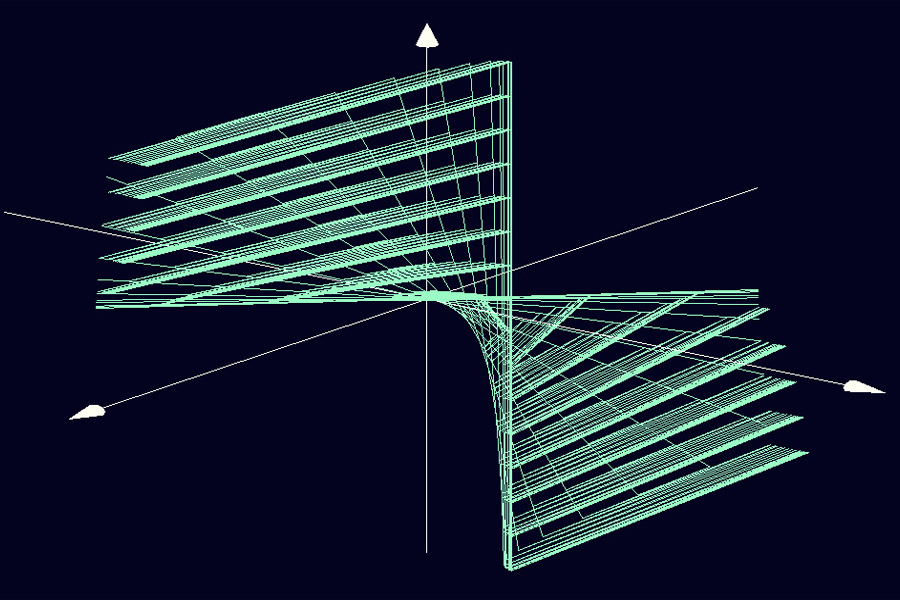
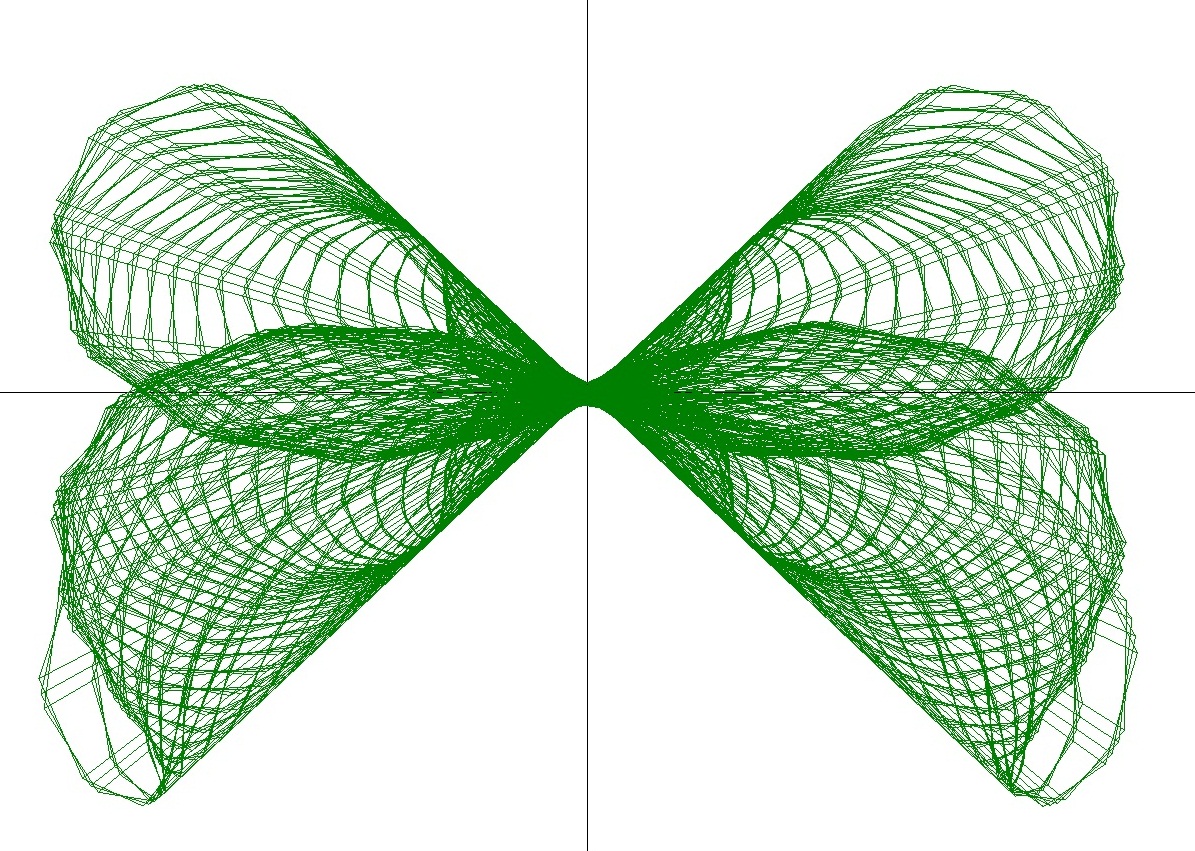
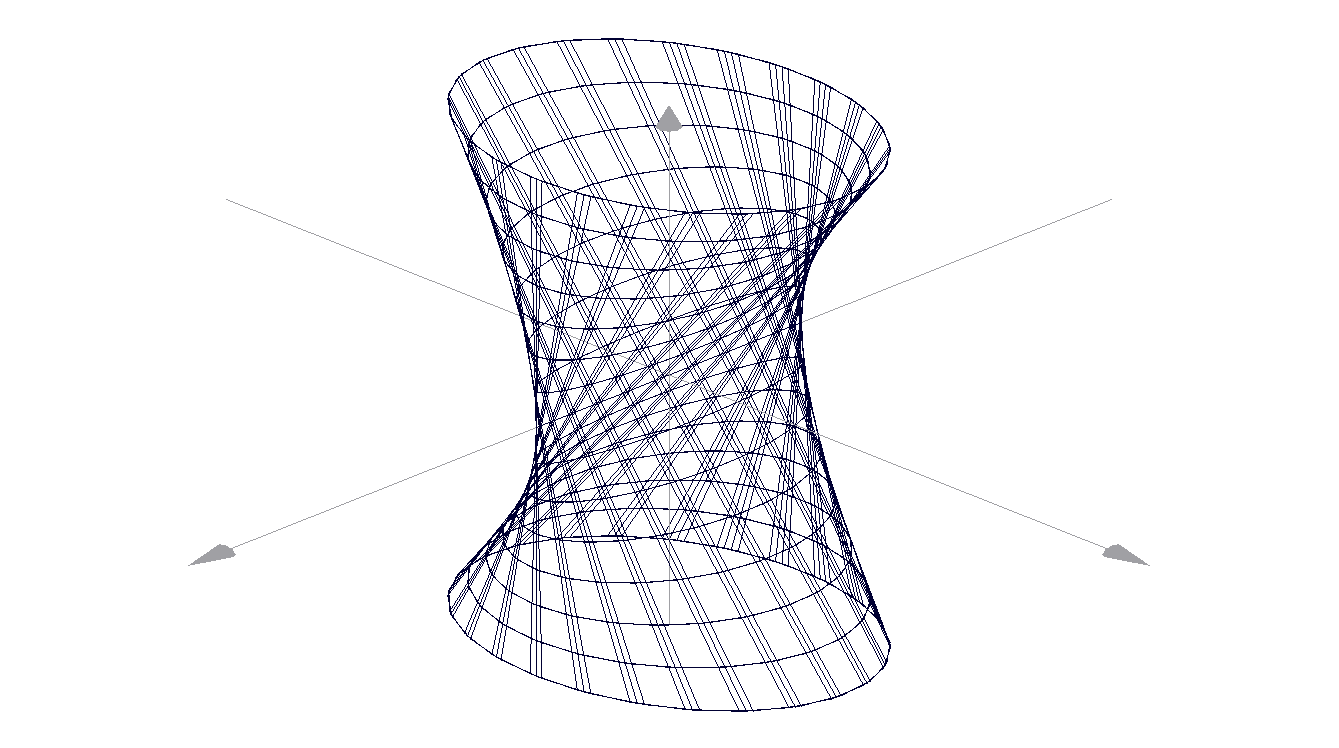
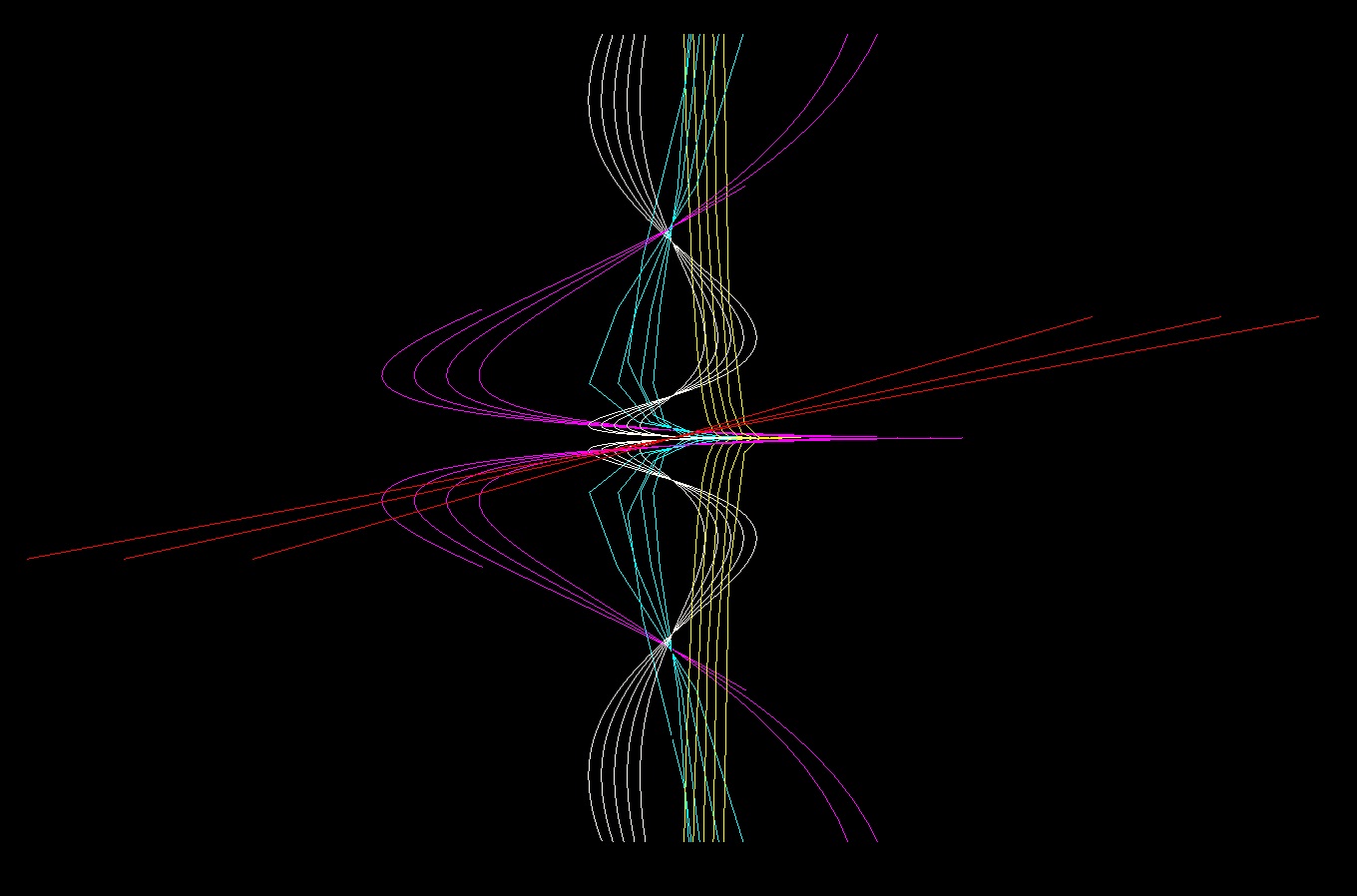
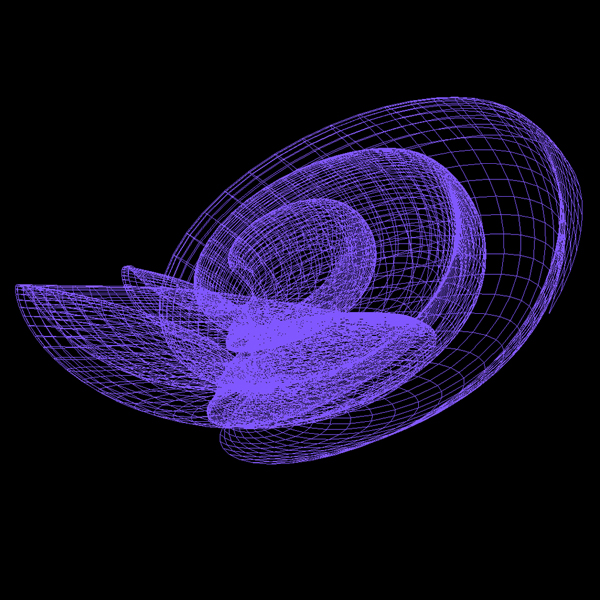
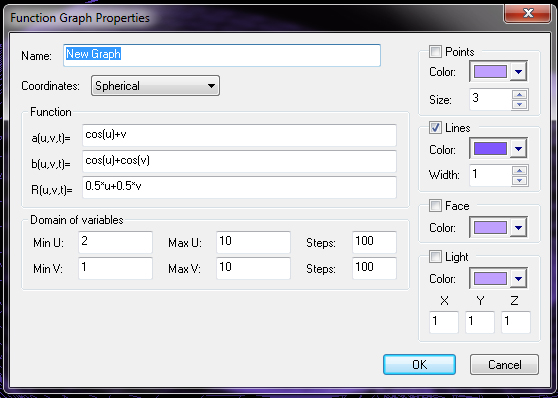
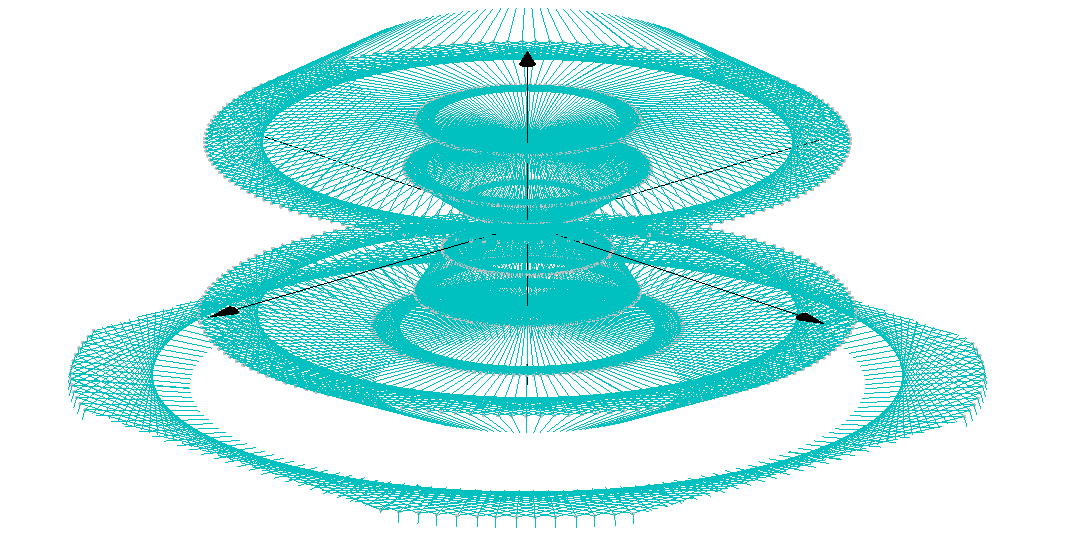
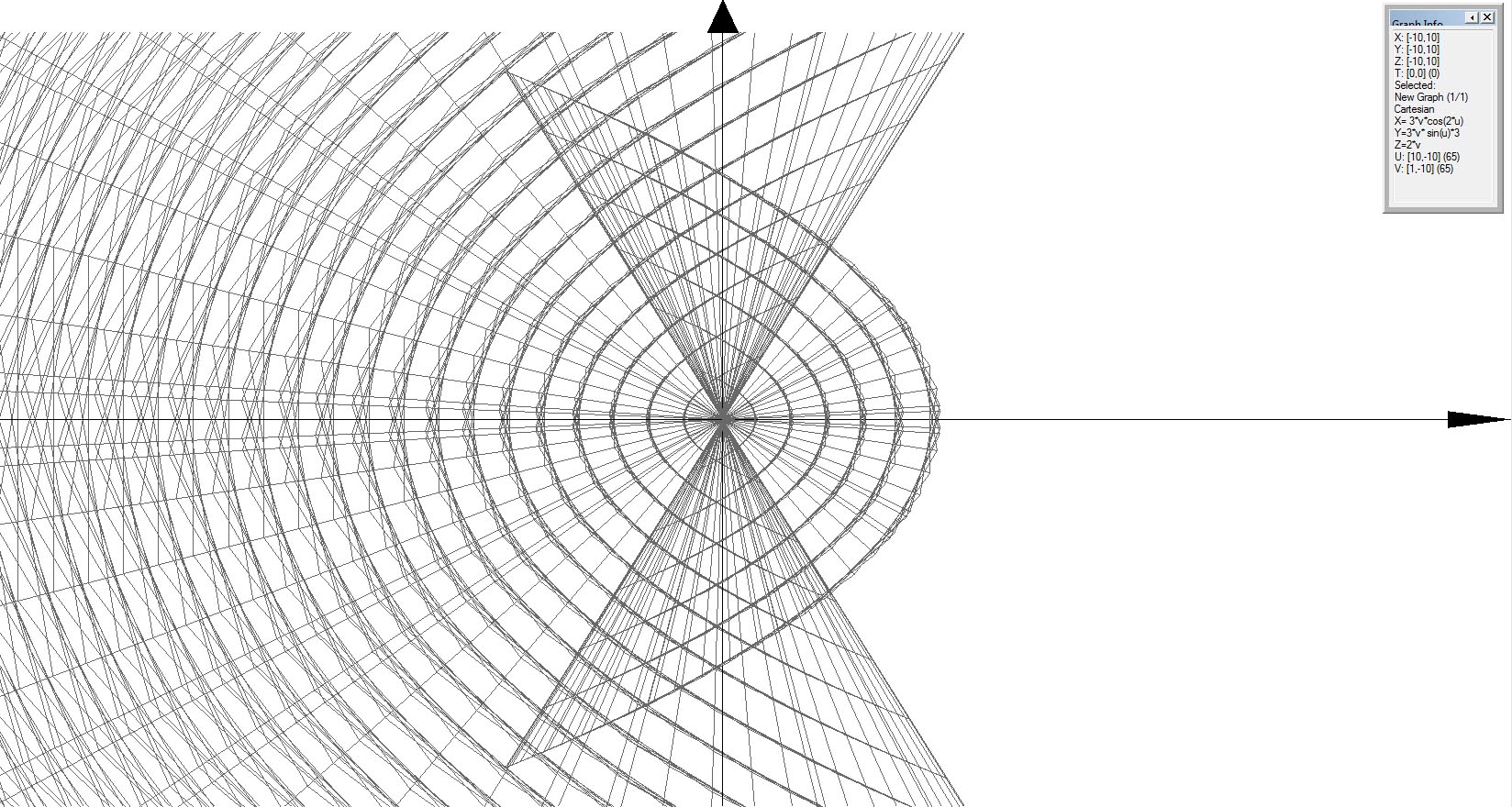
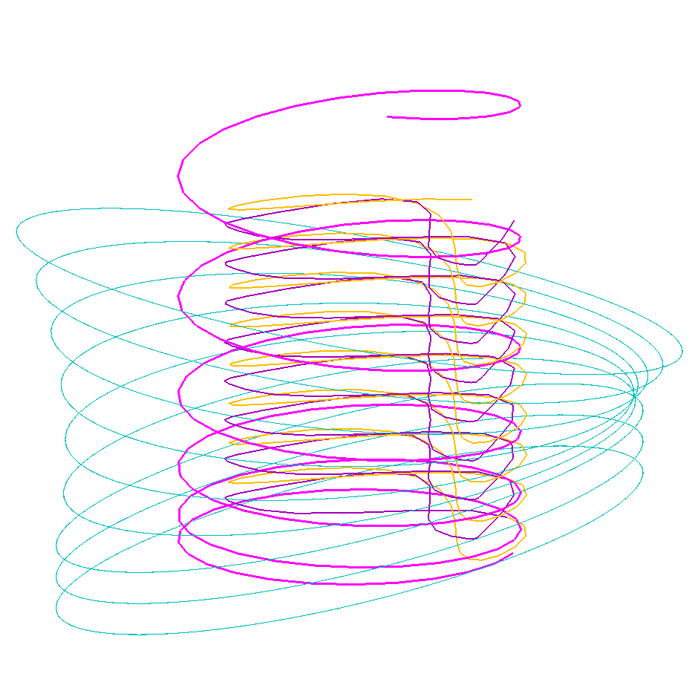
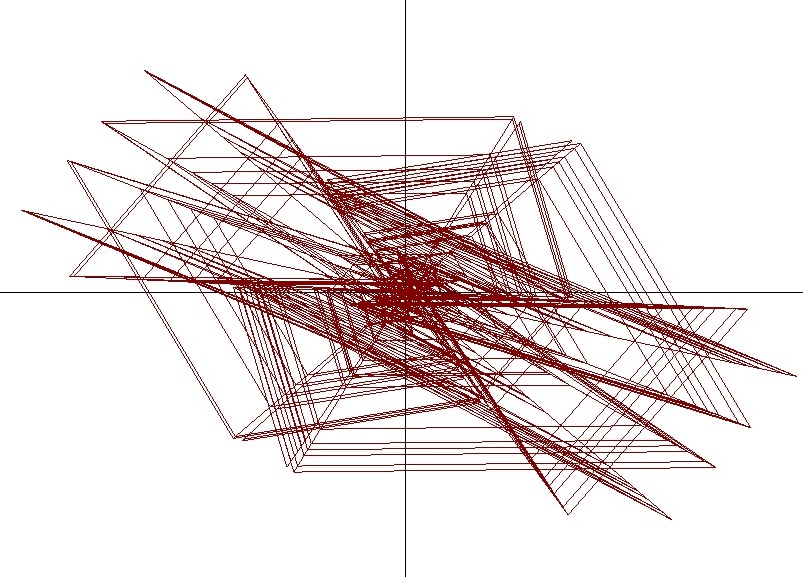
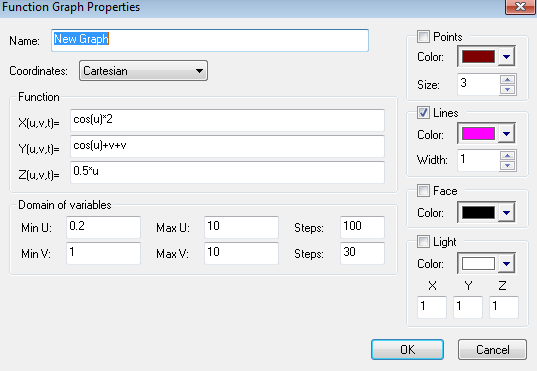
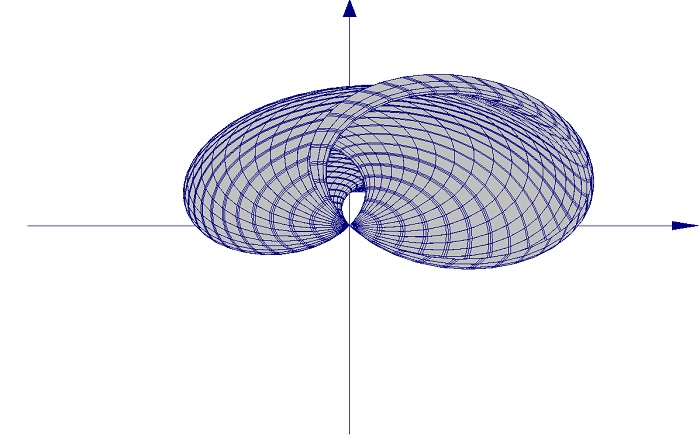
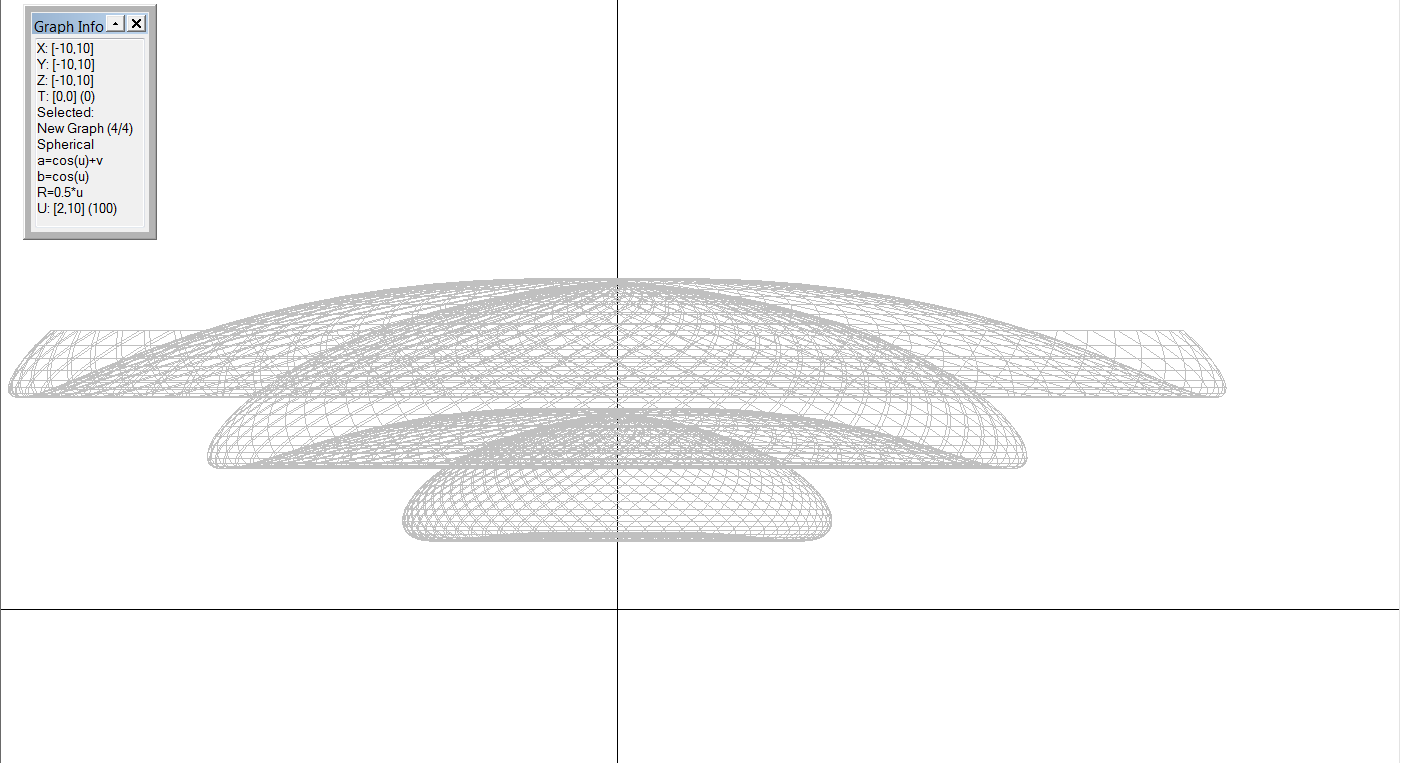
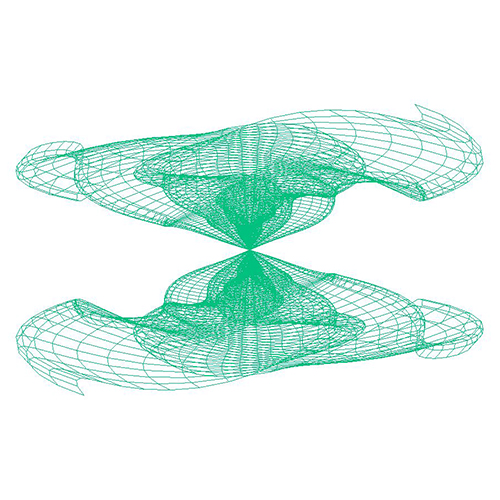
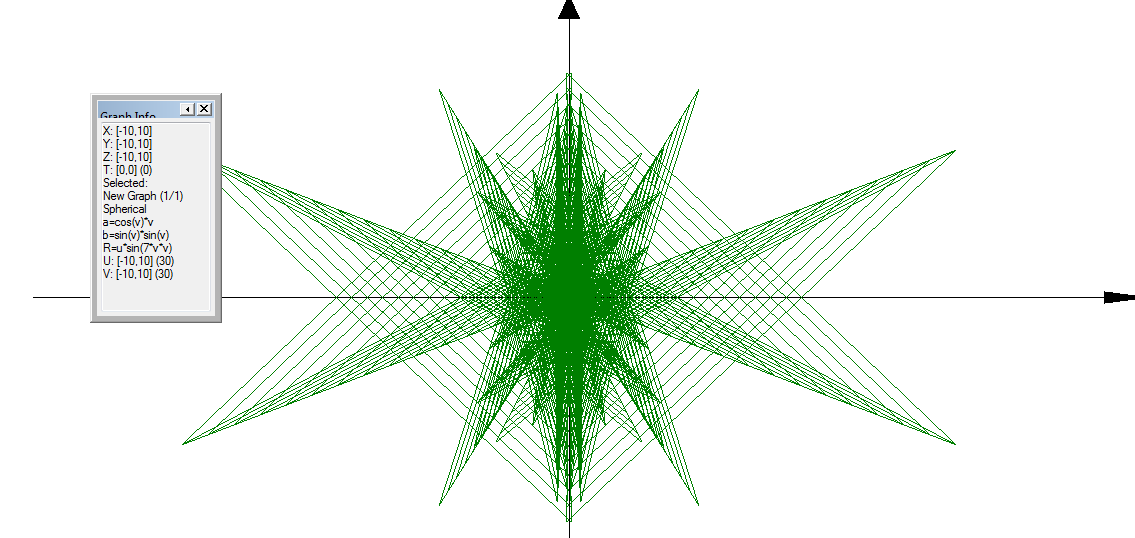
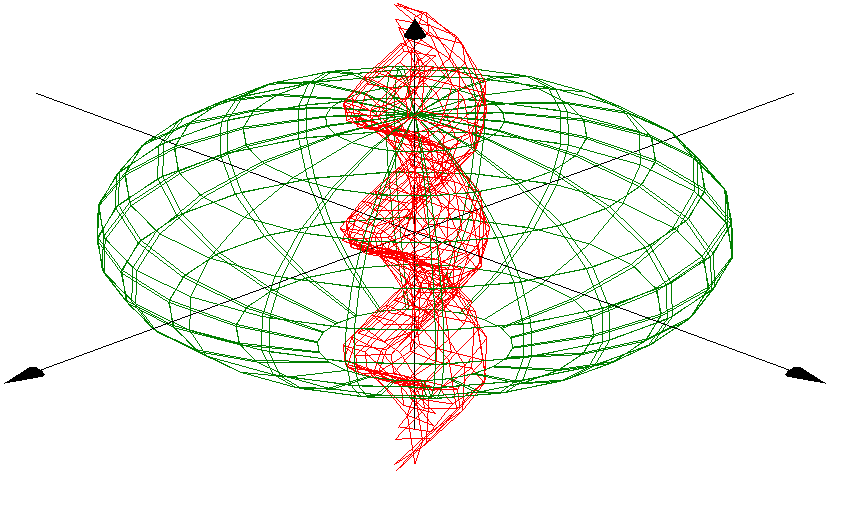
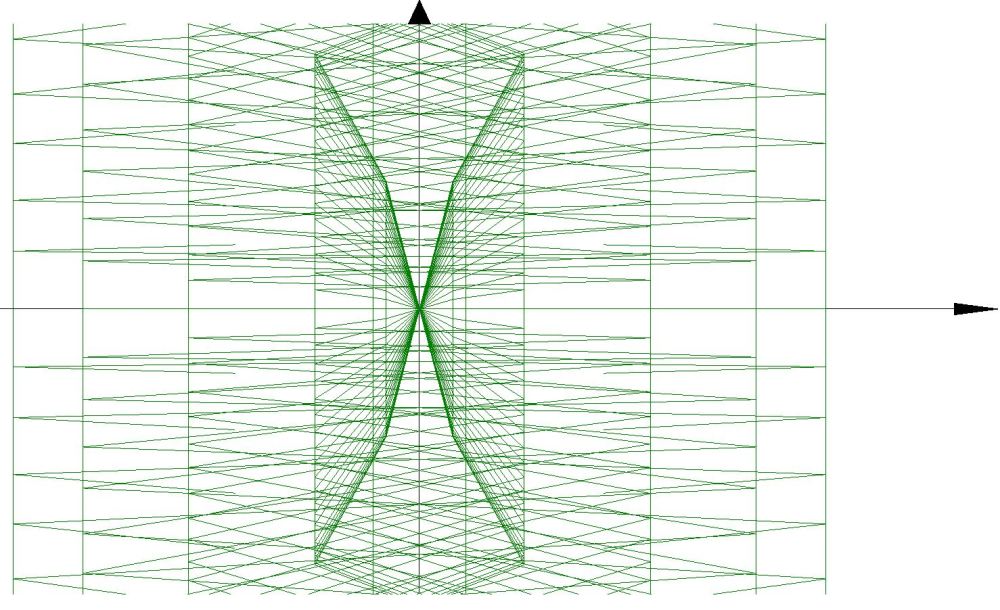
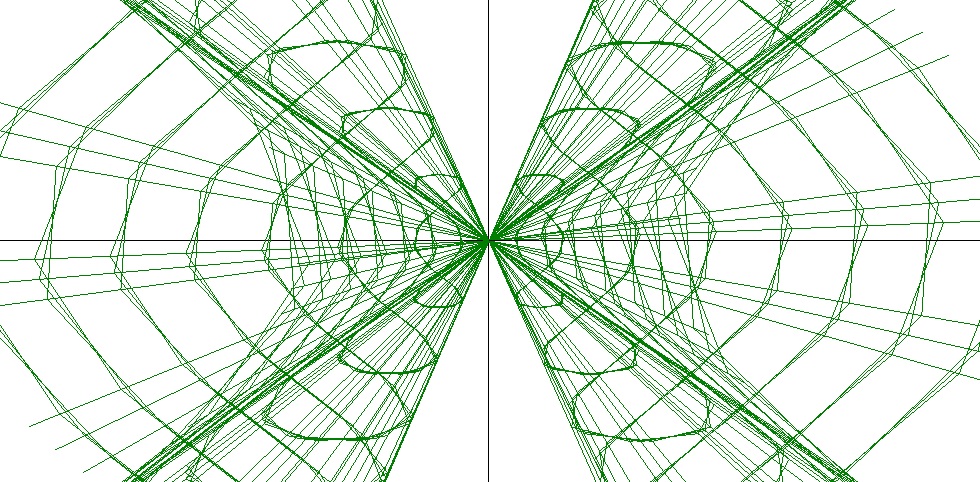
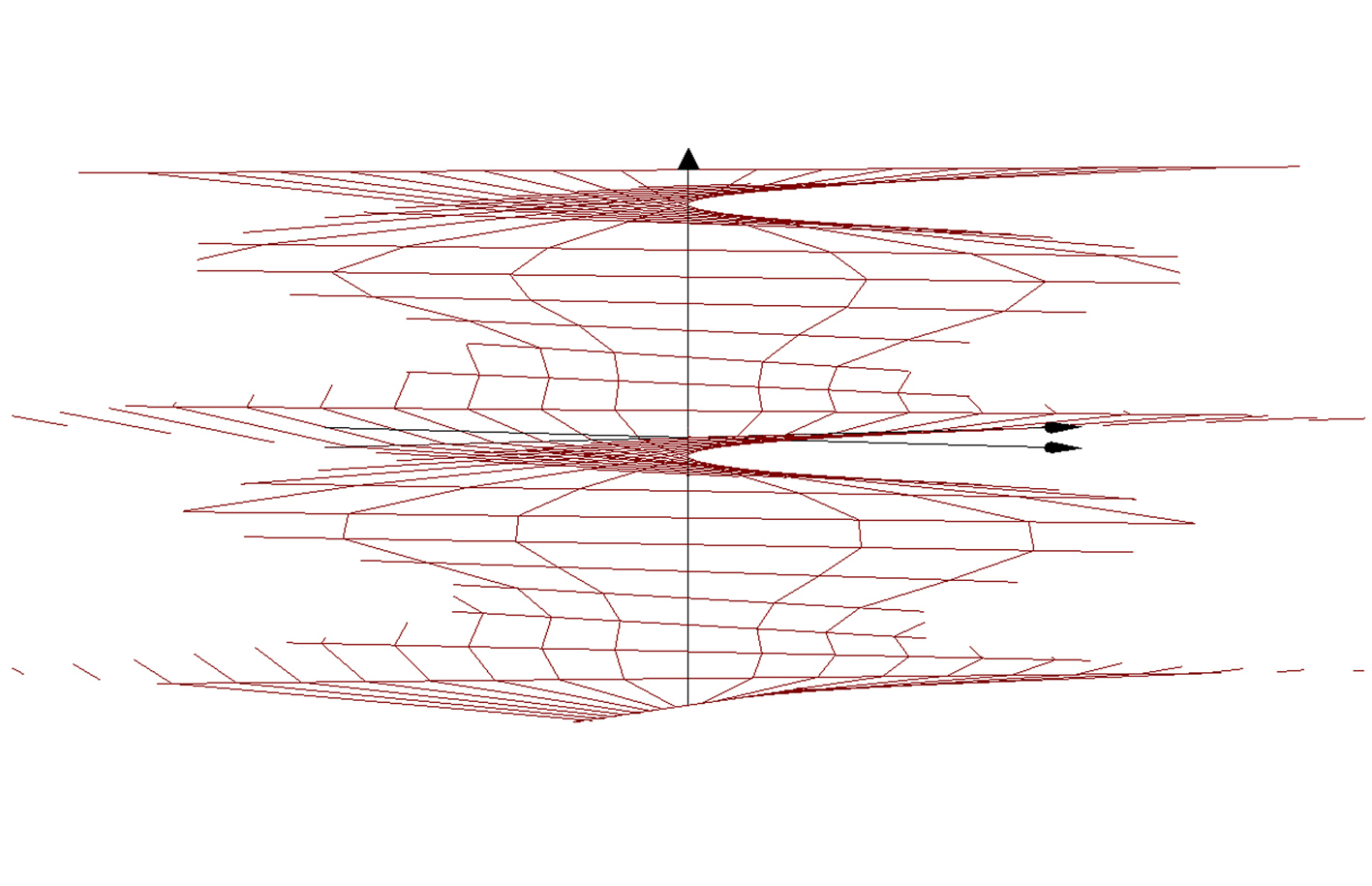
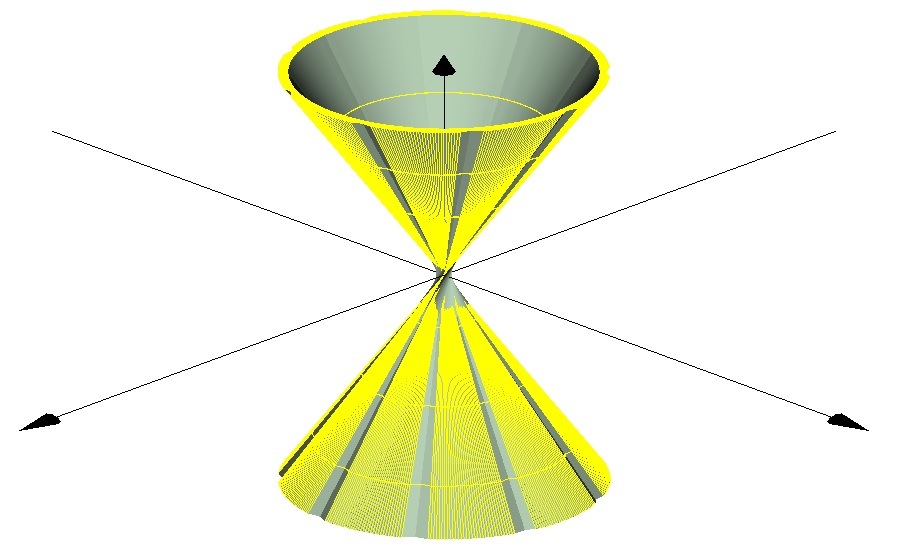
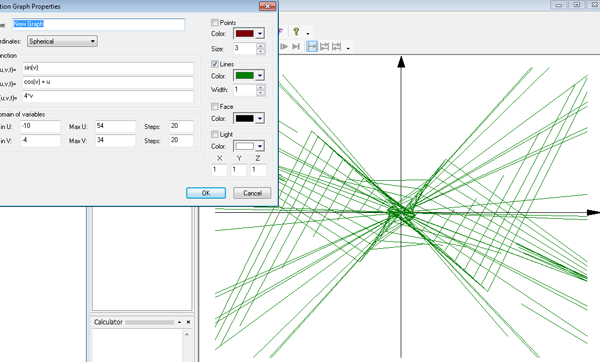
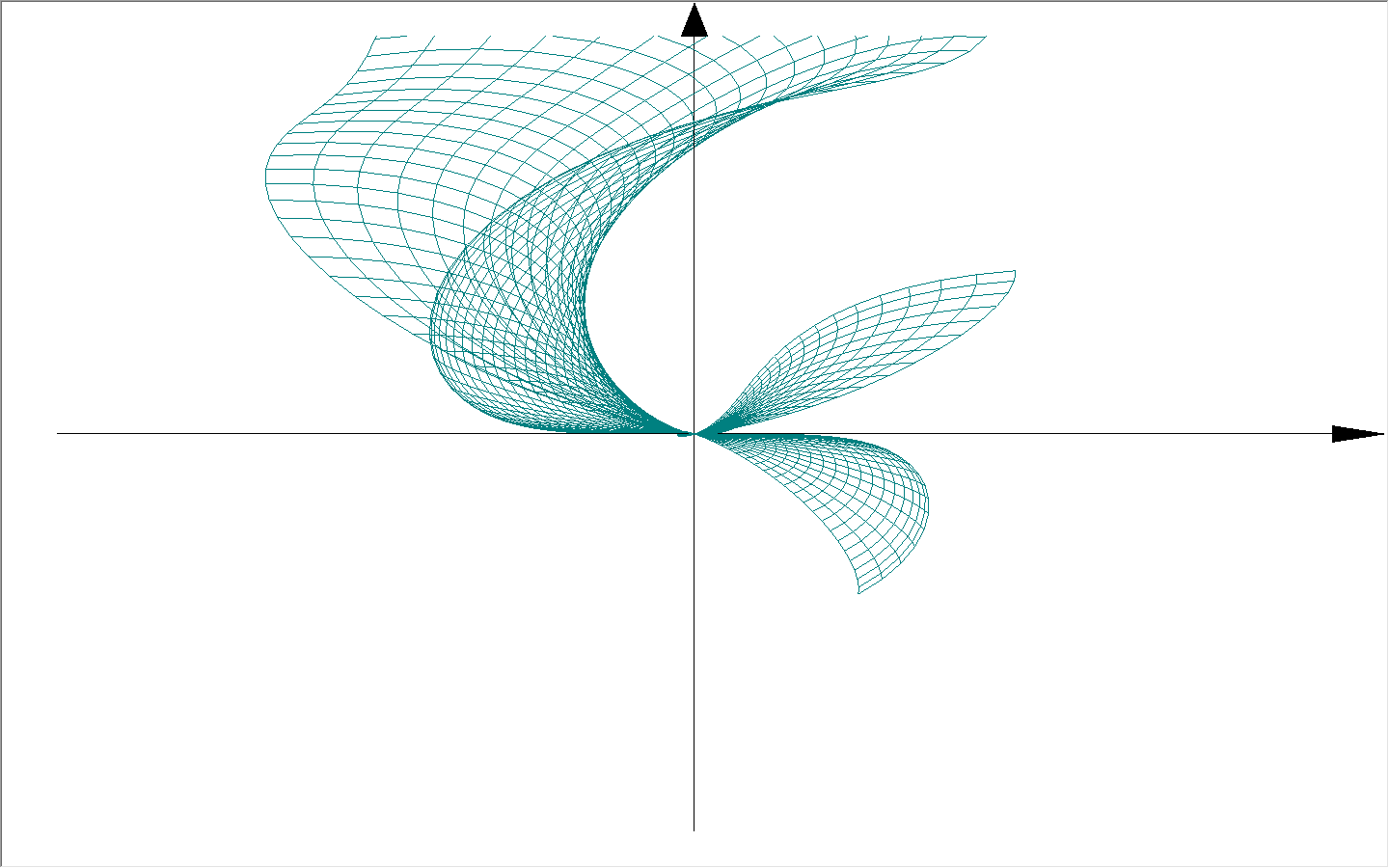
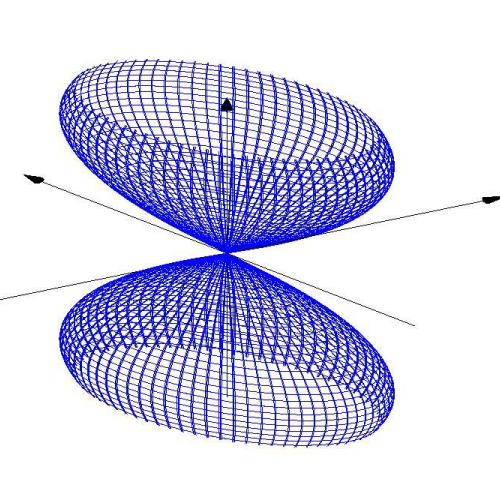
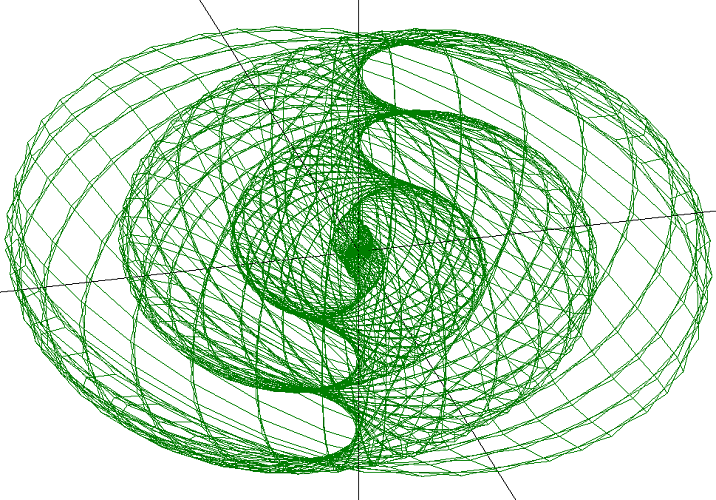
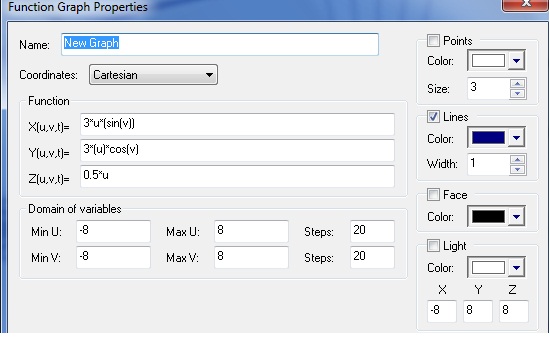
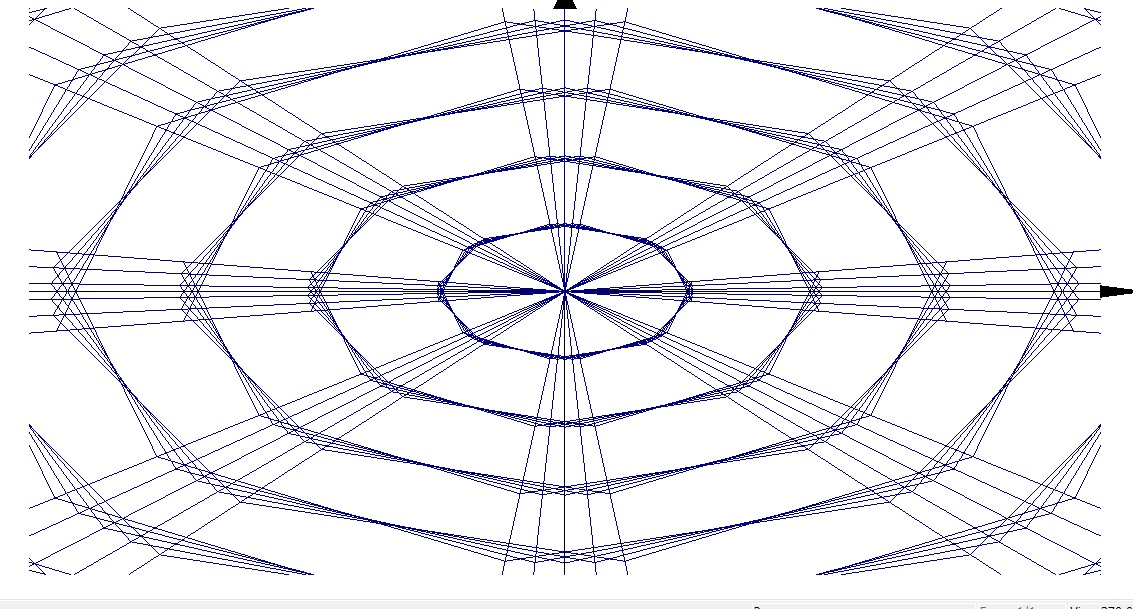
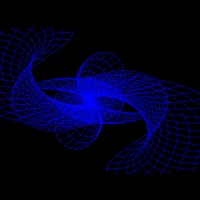
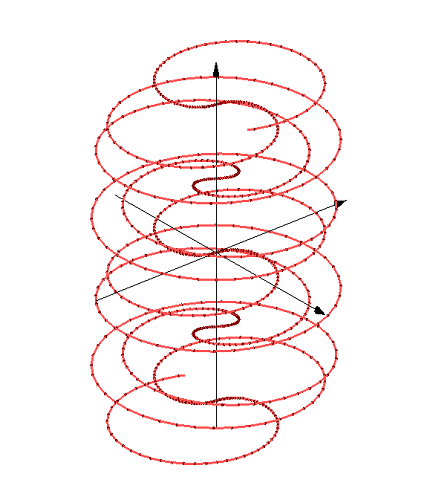
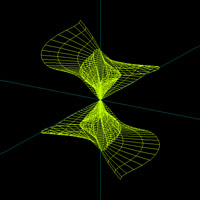
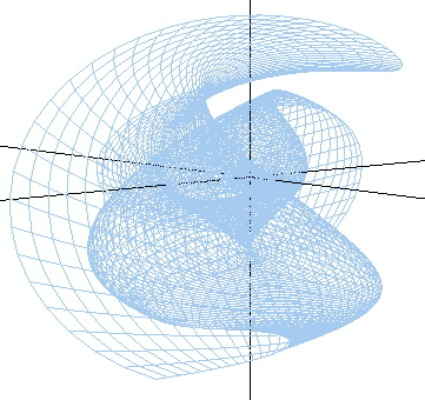
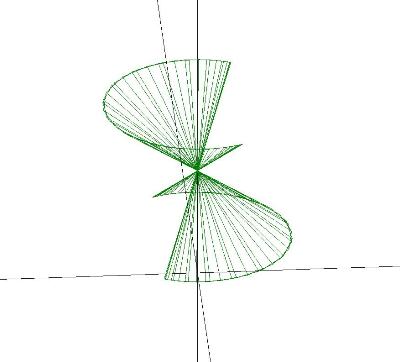
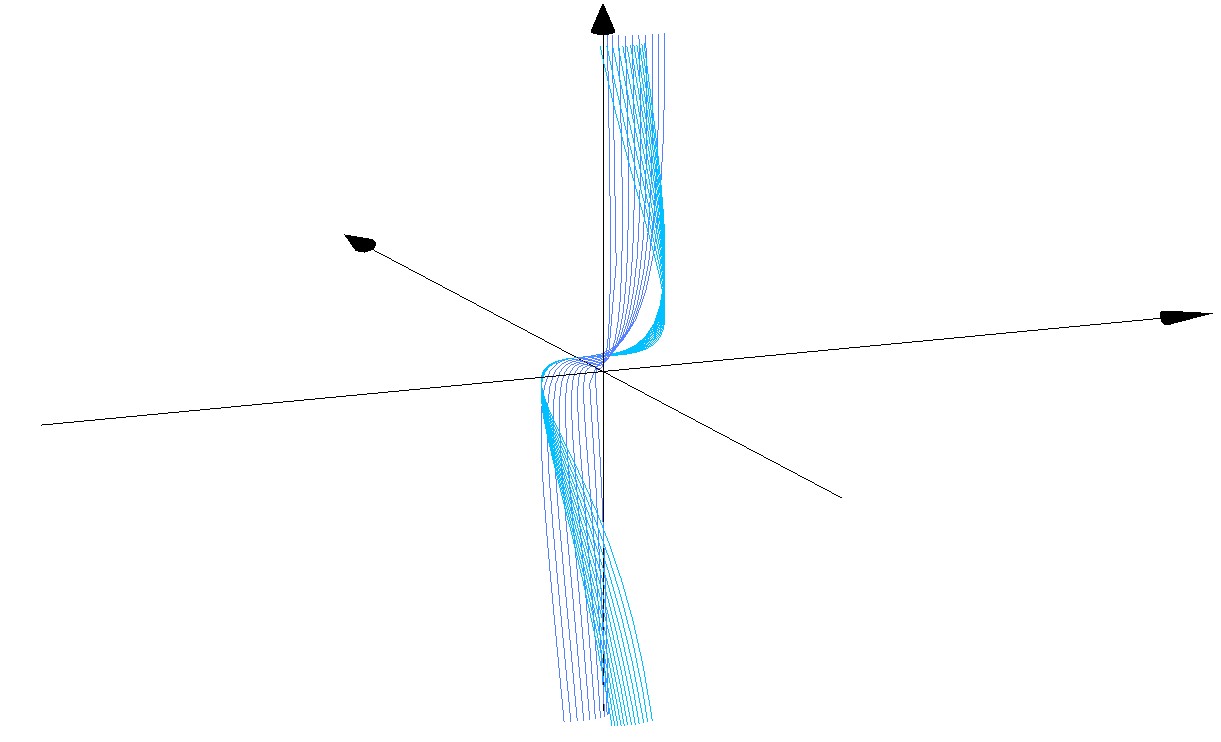
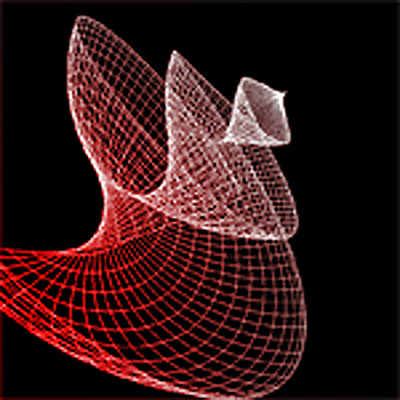
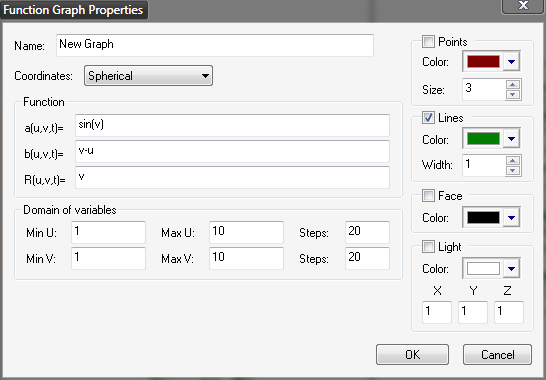
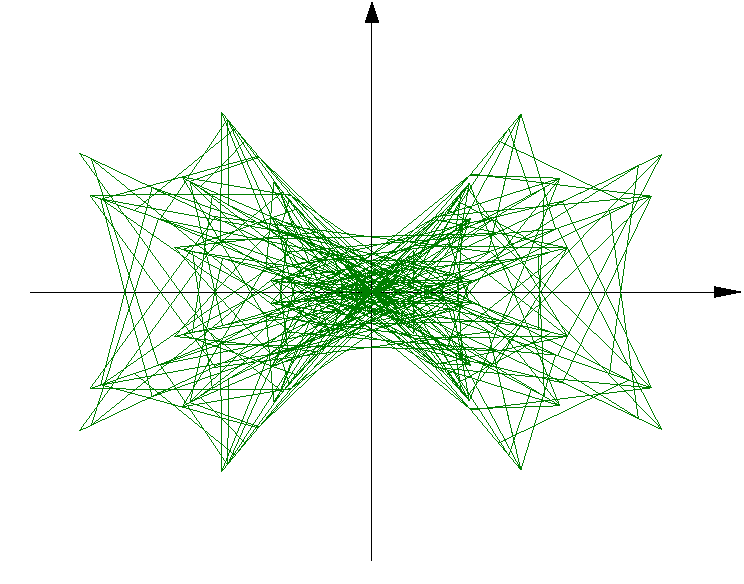
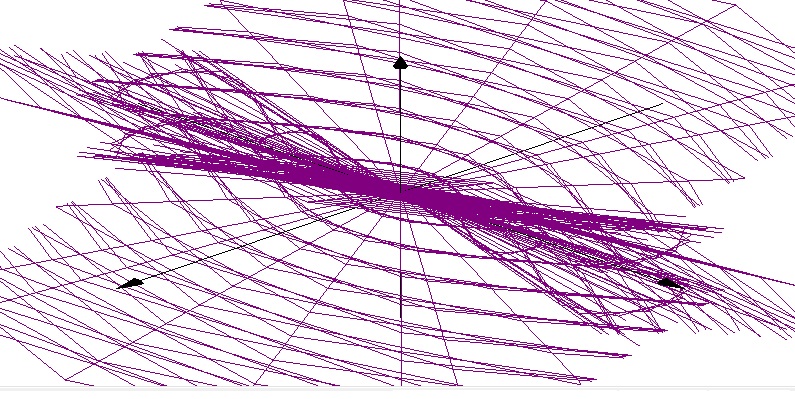
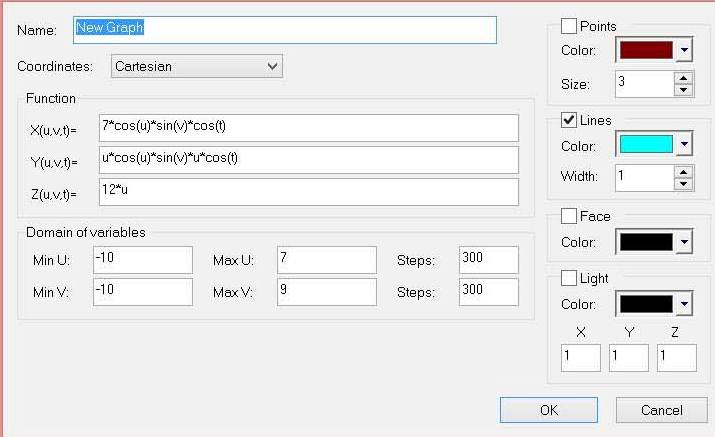
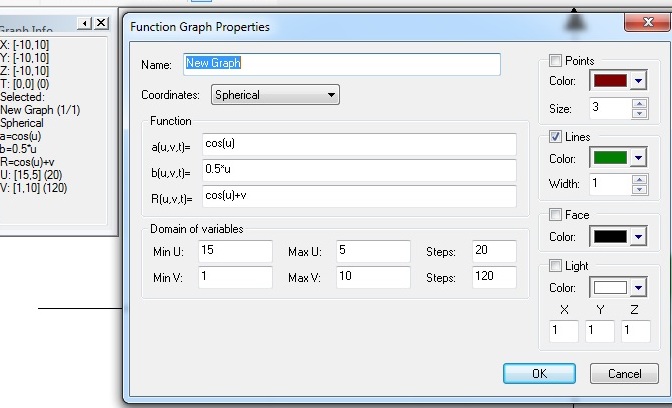
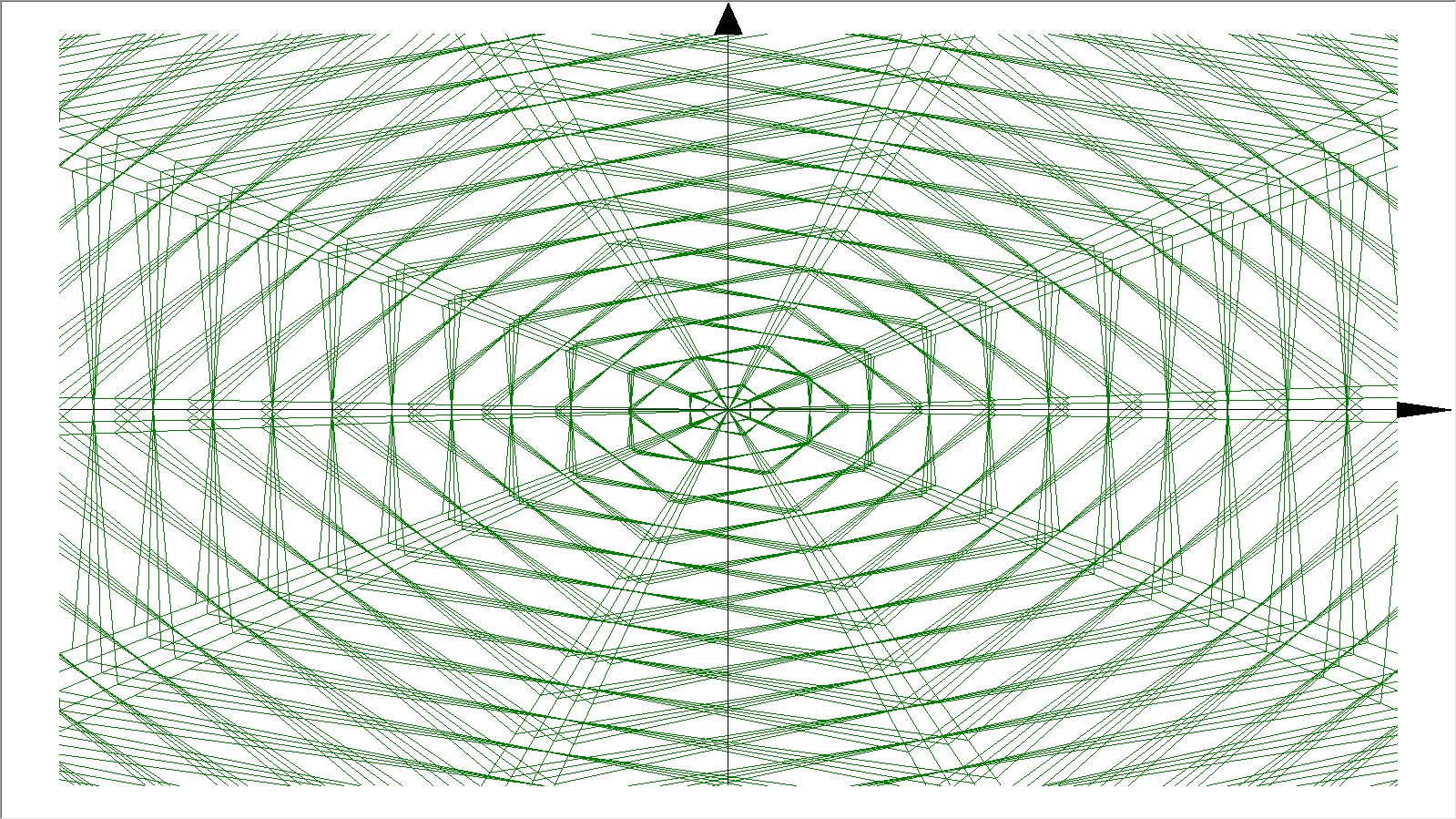
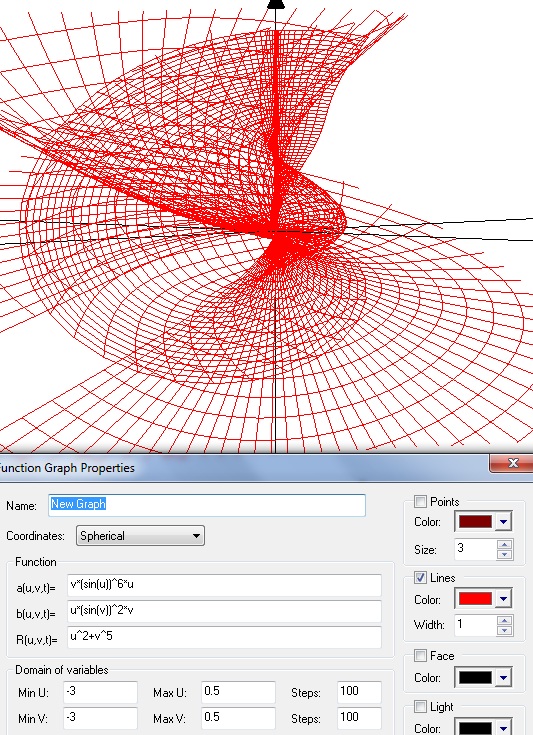
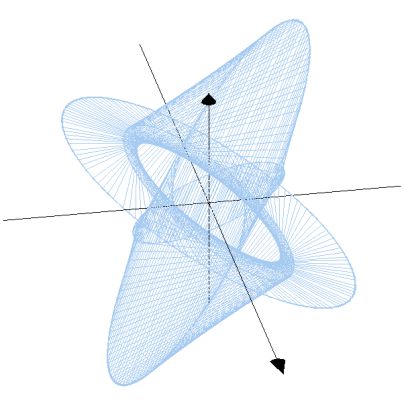
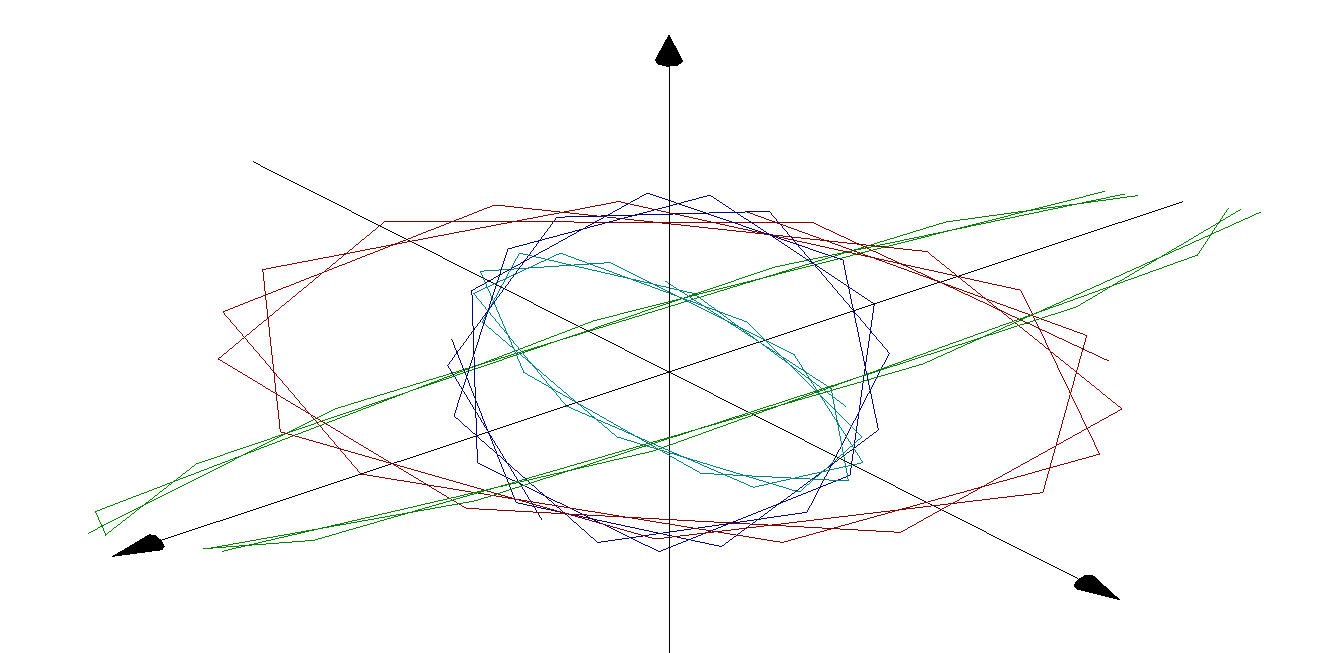
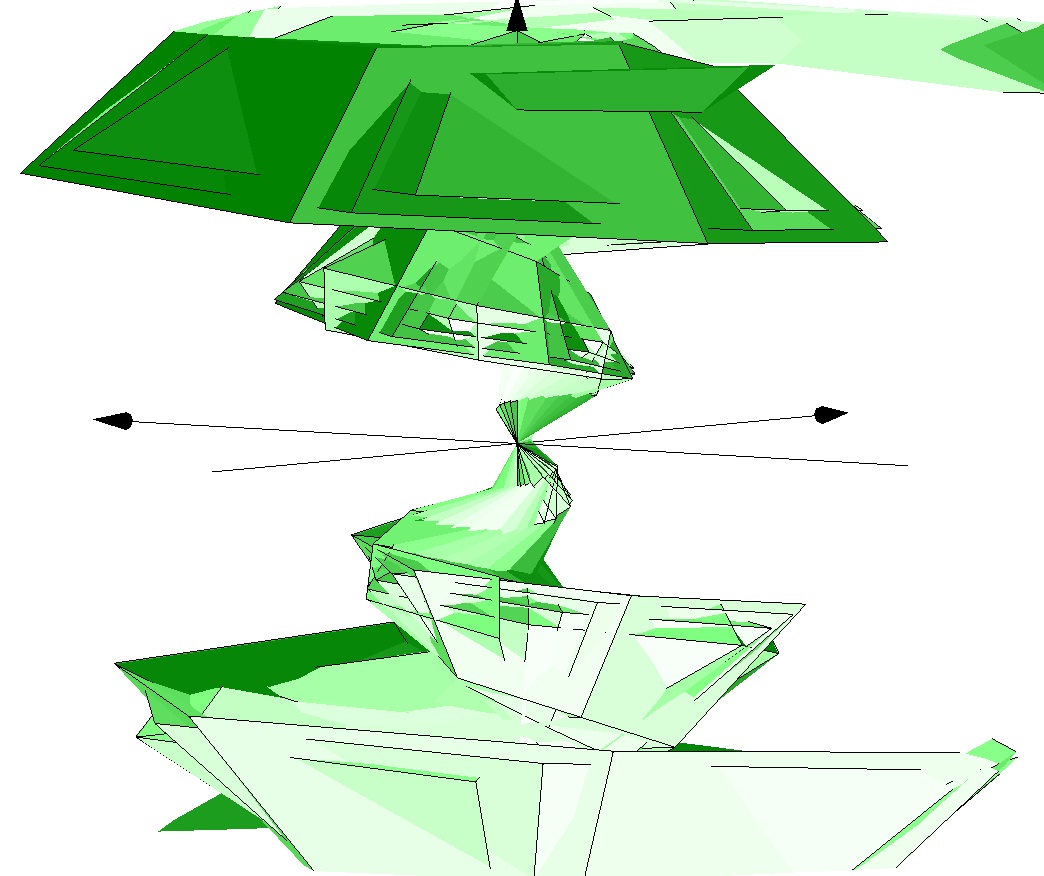
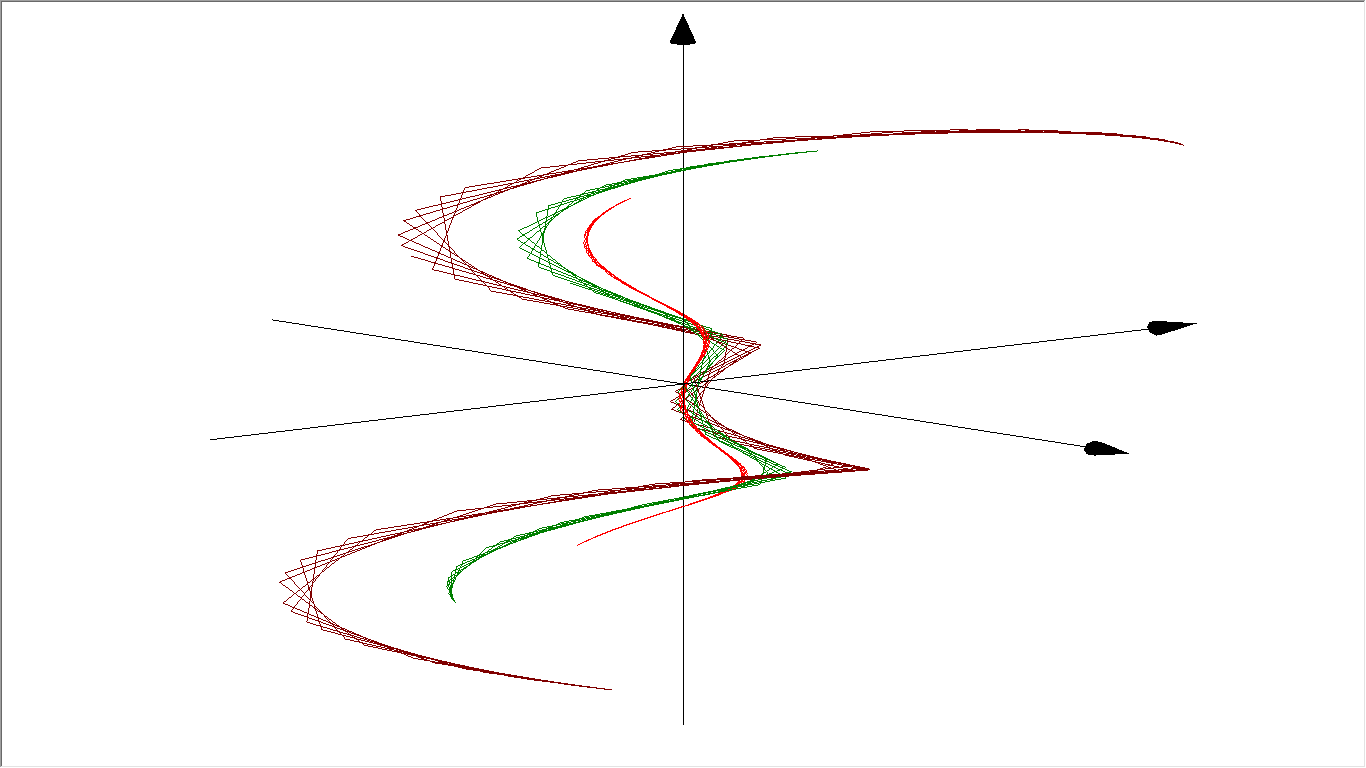
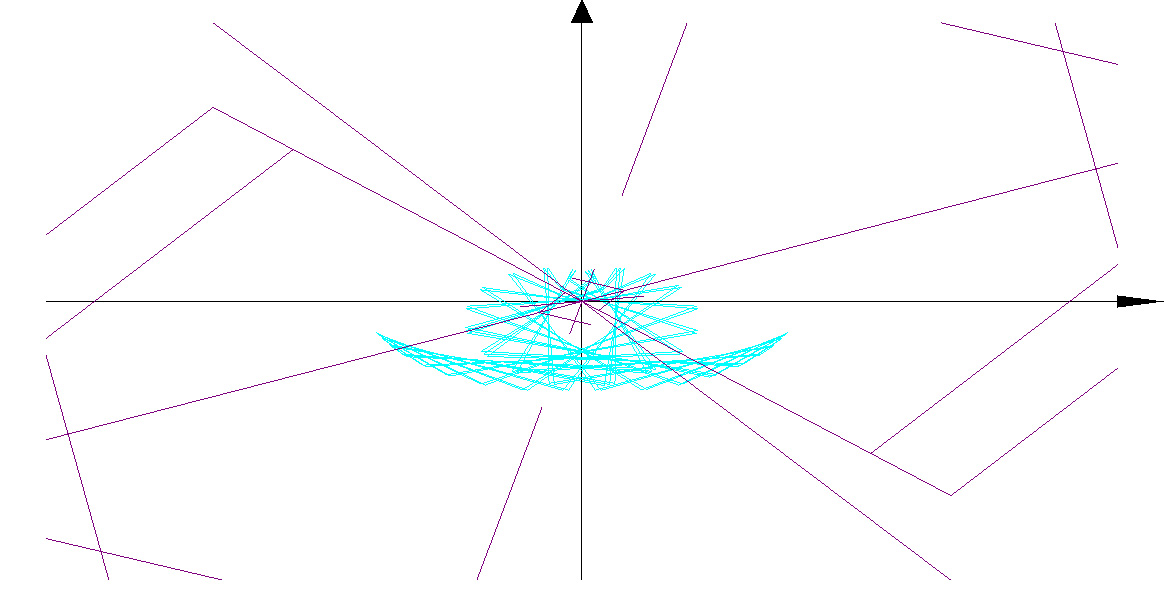
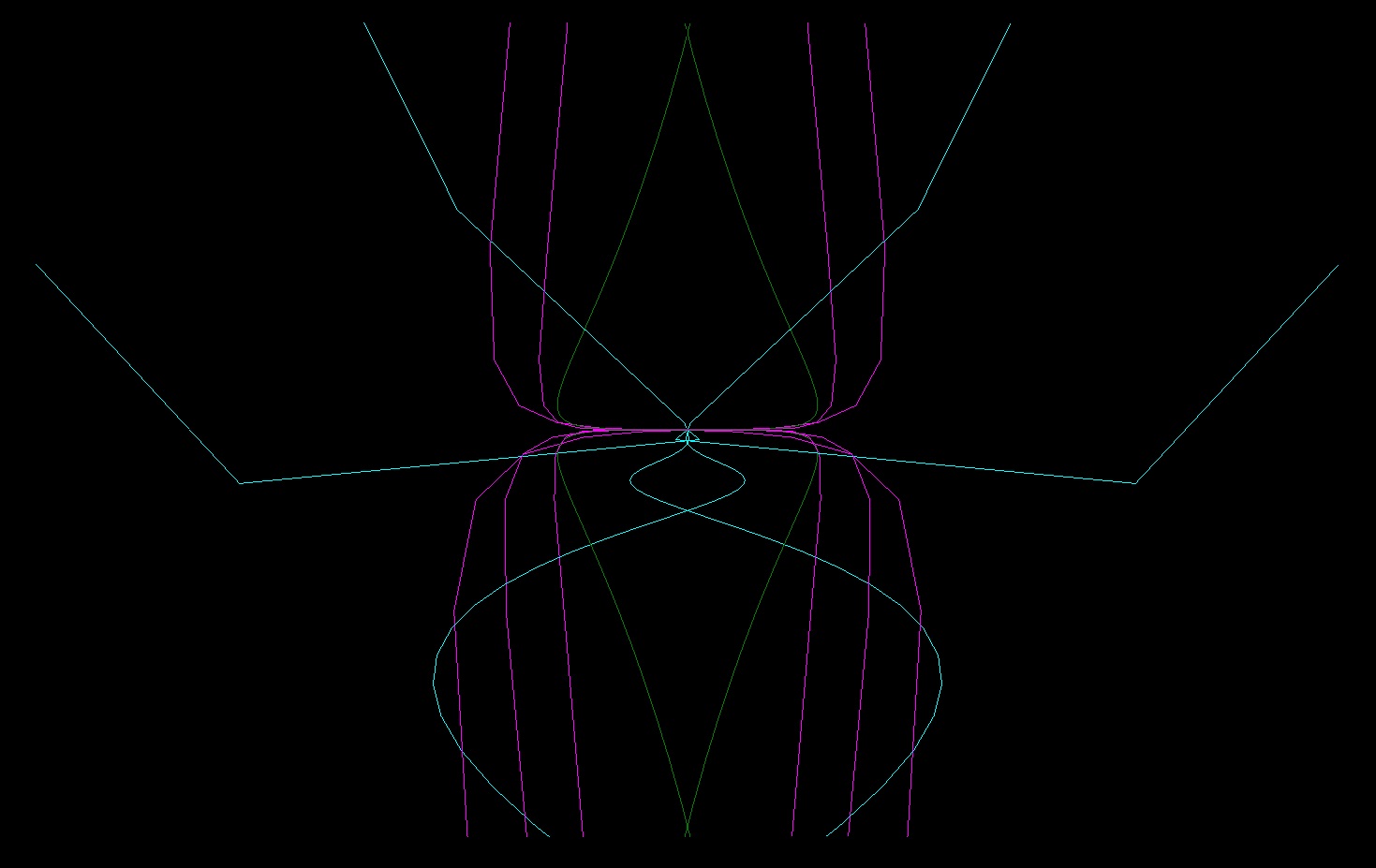
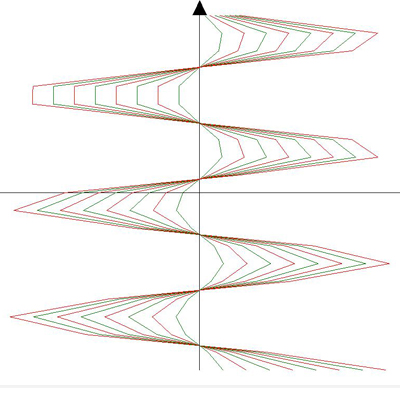
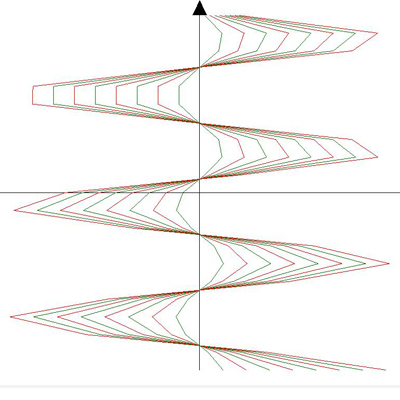
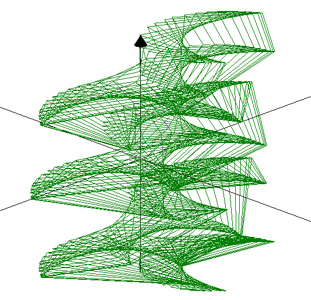
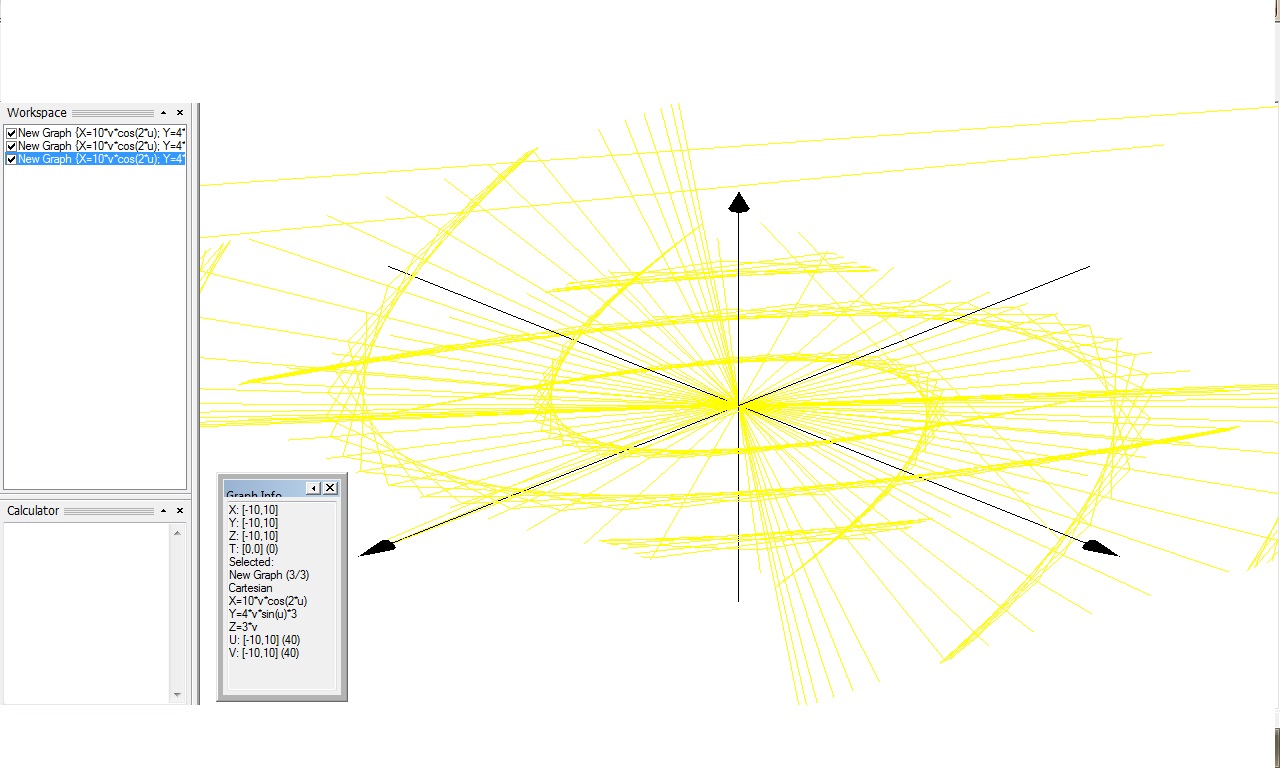
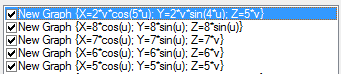
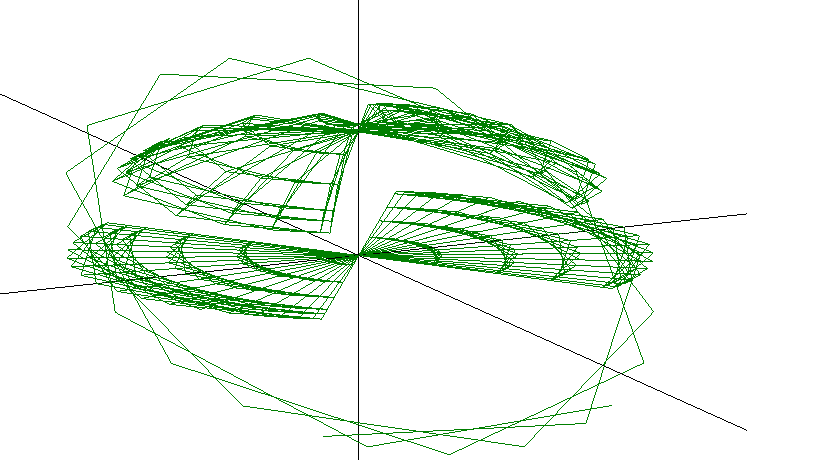
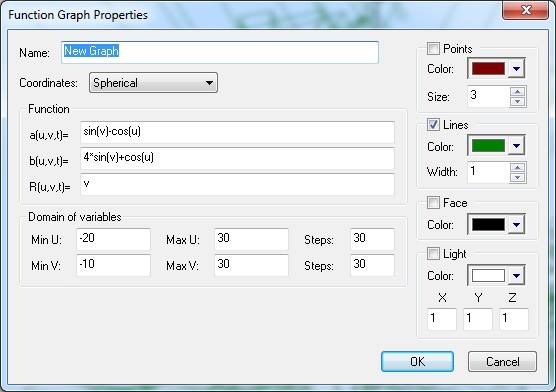
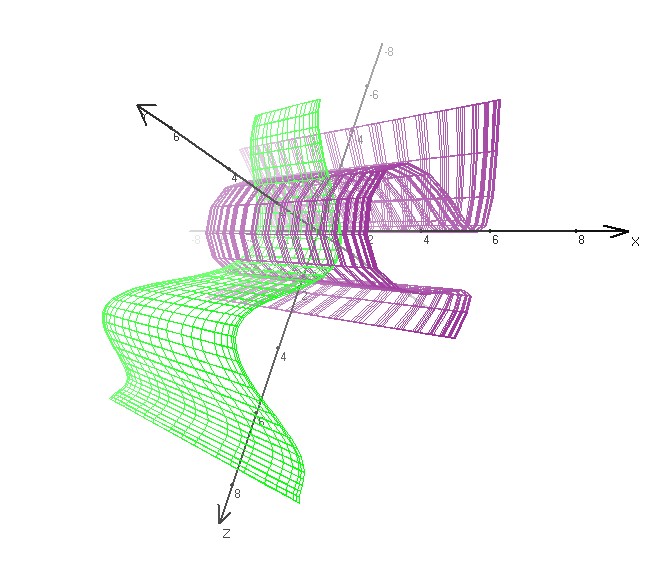
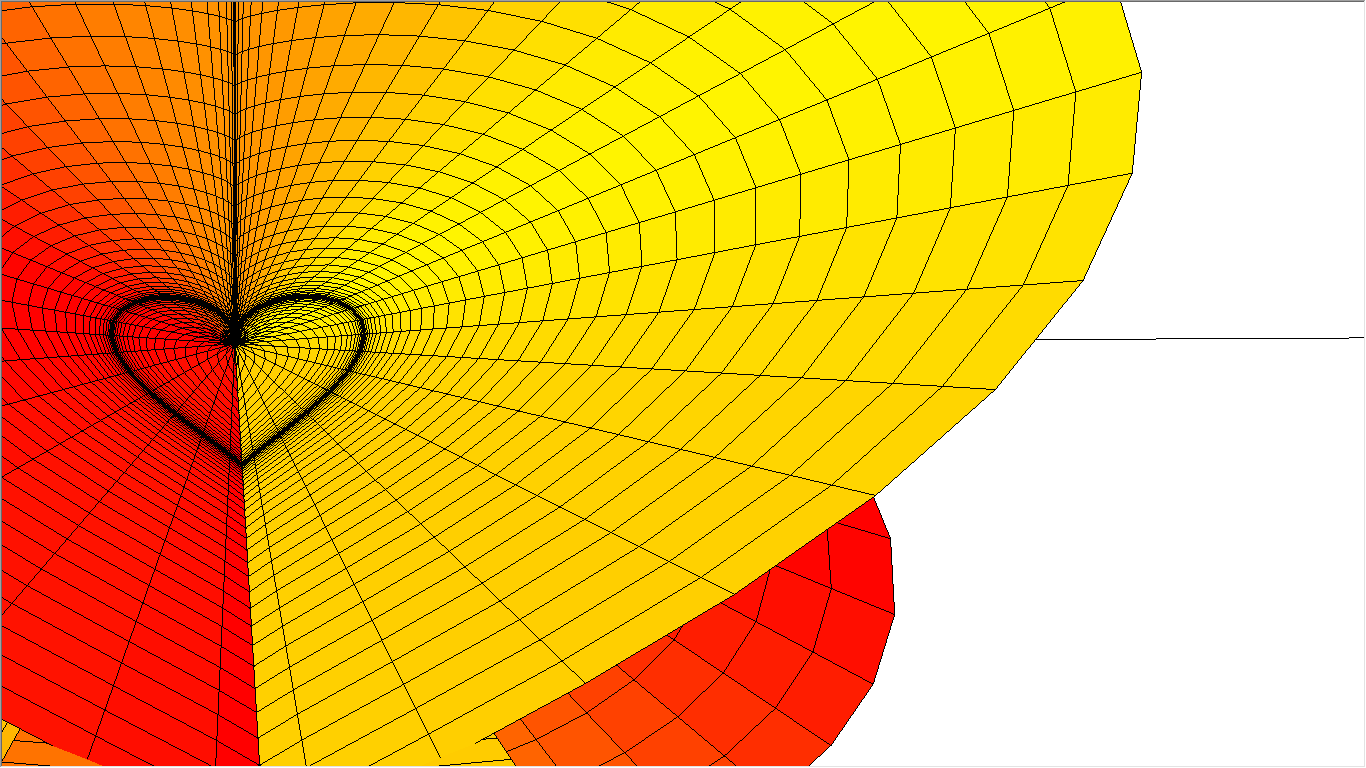
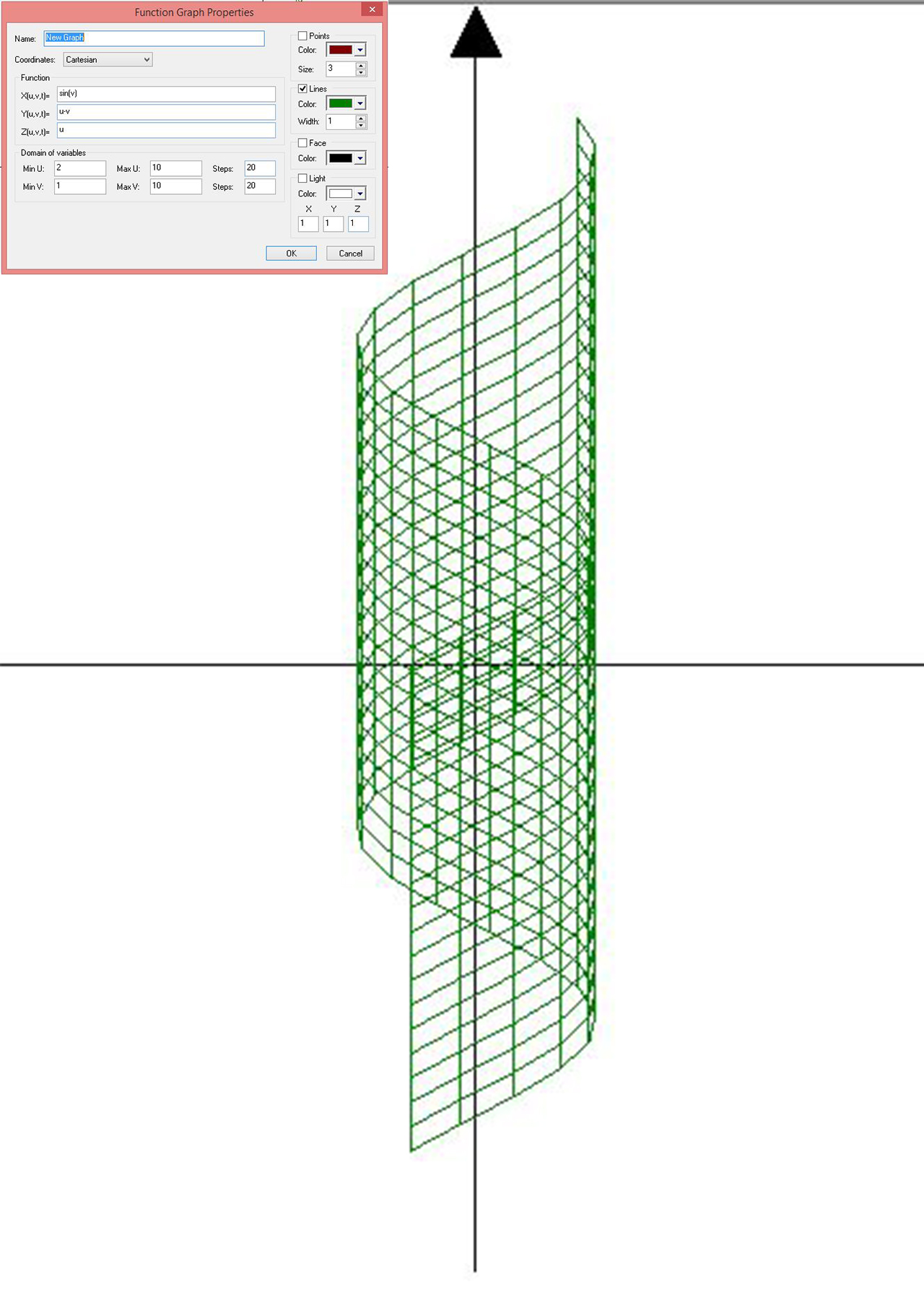
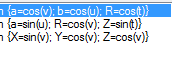3D Grapher.
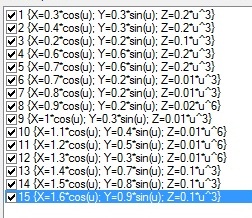
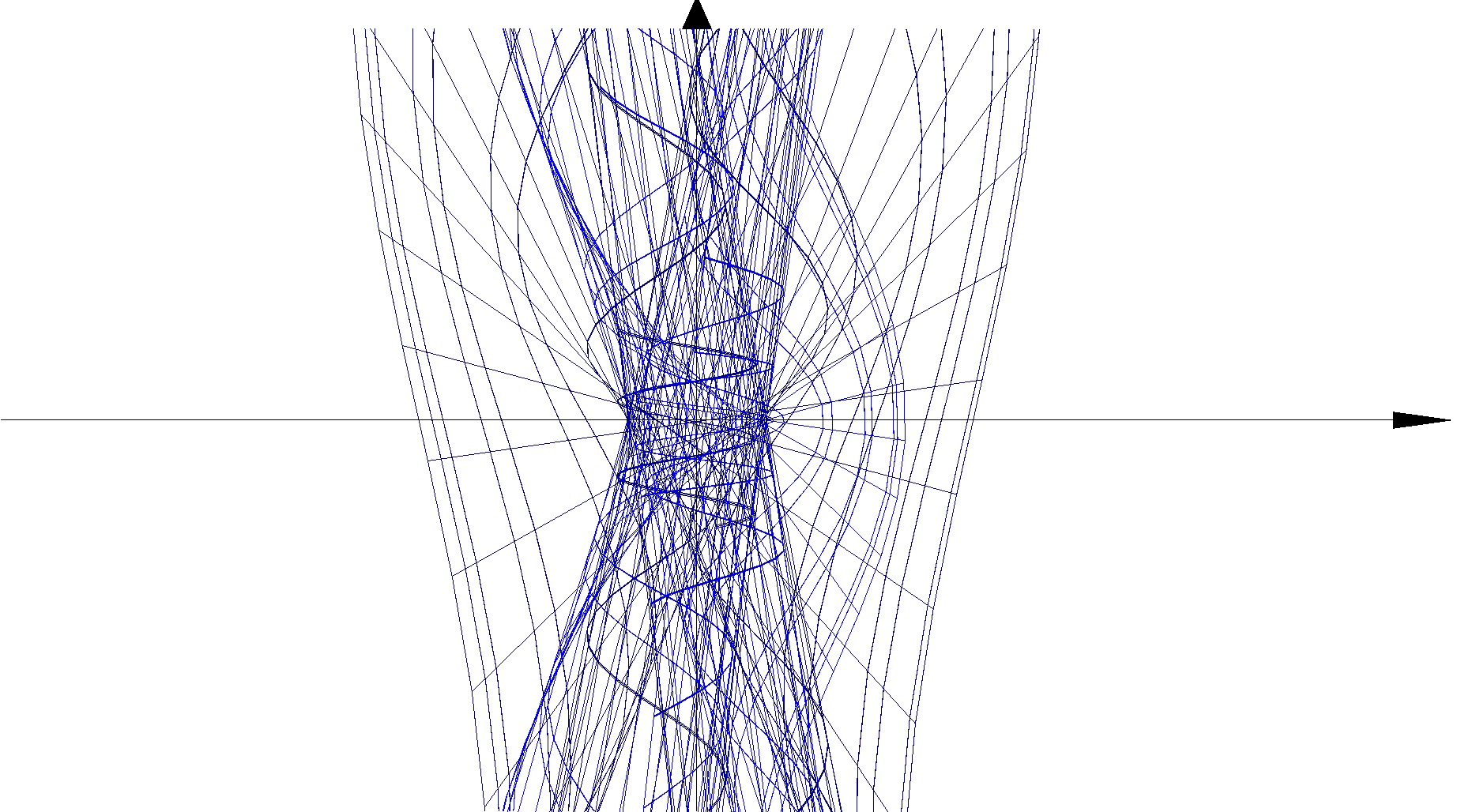
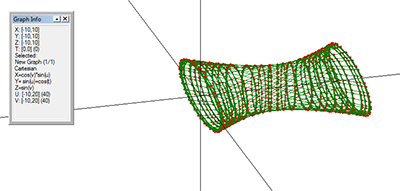
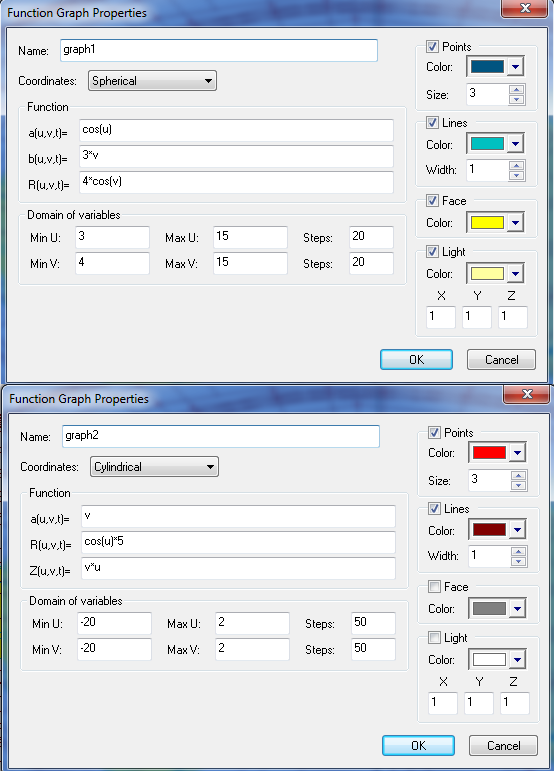
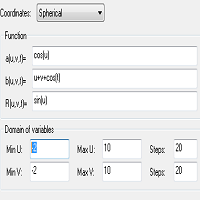
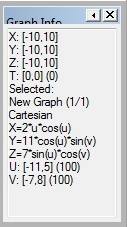
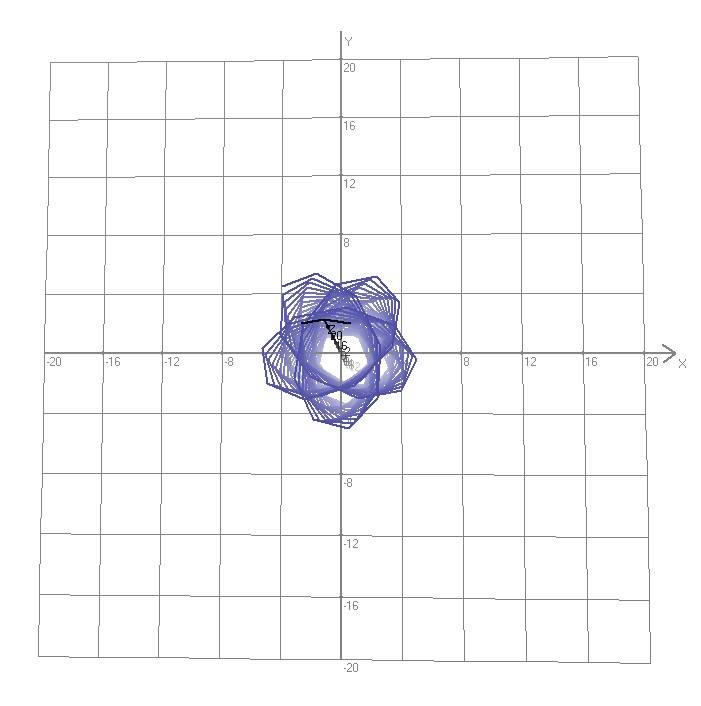
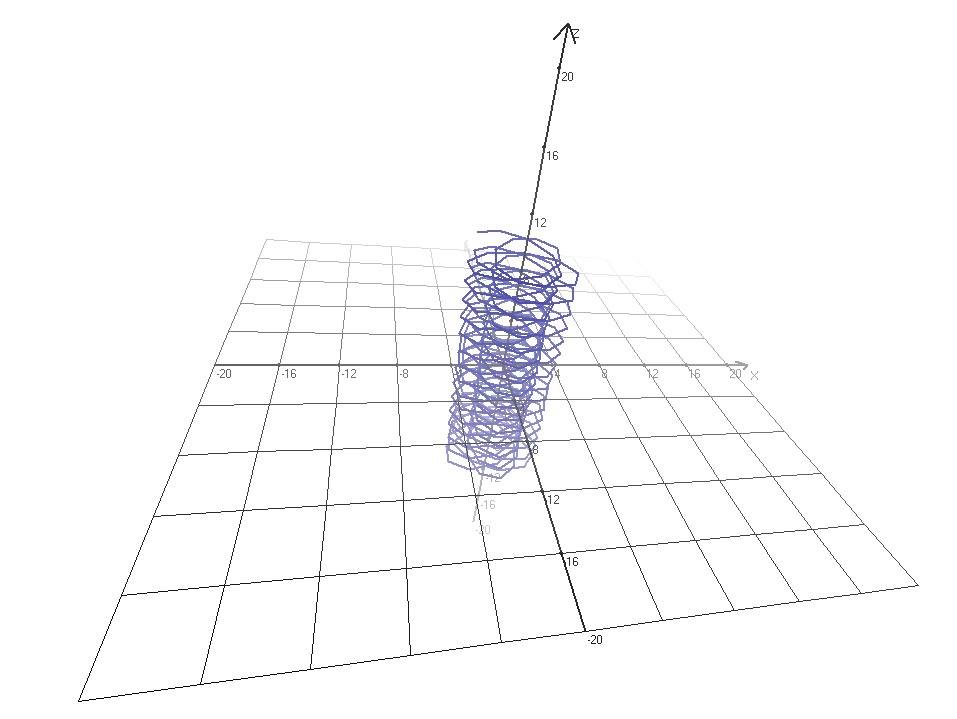
X(u,v,t)= 0.1*sin(u) Y(u,v,t)= 0.2*cos(u) Z(u,v,t)= 0.3*u^3
X(u,v,t)= 0.2*sin(u) Y(u,v,t)= 0.3*cos(u) Z(u,v,t)= 0.4*u^3
X(u,v,t)= 0.3*sin(u) Y(u,v,t)= 0.4*cos(u) Z(u,v,t)= 0.5*u^3
X(u,v,t)= 0.4*sin(u) Y(u,v,t)= 0.5*cos(u) Z(u,v,t)= 0.6*u^3
X(u,v,t)= 0.5*sin(u) Y(u,v,t)= 0.6*cos(u) Z(u,v,t)= 0.7*u^3
X(u,v,t)= 0.6*sin(u) Y(u,v,t)= 0.7*cos(u) Z(u,v,t)= 0.8*u^3
X(u,v,t)= 0.7*sin(u) Y(u,v,t)= 0.8*cos(u) Z(u,v,t)= 0.9*u^3
X(u,v,t)= 0.8*sin(u) Y(u,v,t)= 0.9*cos(u) Z(u,v,t)= 1*u^3
X(u,v,t)= 0.9*sin(u) Y(u,v,t)= 1*cos(u) Z(u,v,t)= 1.1*u^3
X(u,v,t)= 1*sin(u) Y(u,v,t)= 1.1*cos(u) Z(u,v,t)= 1.2*u^3
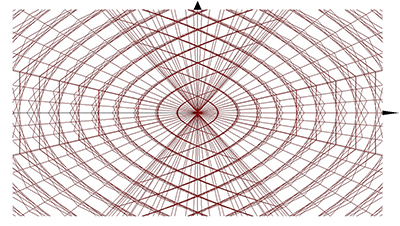
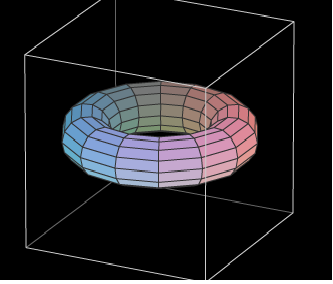
X(u,v,t)= 1*sin(u) Y(u,v,t)= 1.1*cos(u) Z(u,v,t)= 0.21*u^3
X(u,v,t)= 1*sin(u) Y(u,v,t)= 1.1*cos(u) Z(u,v,t)= 0.23*u^3
X(u,v,t)= 1*sin(u) Y(u,v,t)= 1.1*cos(u) Z(u,v,t)= 0.25*u^3
X(u,v,t)= 1*sin(u) Y(u,v,t)= 1.1*cos(u) Z(u,v,t)= 0.27*u^3
X(u,v,t)= 1*sin(u) Y(u,v,t)= 1.1*cos(u) Z(u,v,t)= 0.29*u^3
X(u,v,t)= 1*sin(u) Y(u,v,t)= 1.1*cos(u) Z(u,v,t)= 0.31*u^3
X(u,v,t)= 1*sin(u) Y(u,v,t)= 1.1*cos(u) Z(u,v,t)= 0.33*u^3
X(u,v,t)= 1*sin(u) Y(u,v,t)= 1.1*cos(u) Z(u,v,t)= 0.35*u^3
X(u,v,t)= 1*sin(u) Y(u,v,t)= 1.1*cos(u) Z(u,v,t)= 0.37*u^3
X(u,v,t)= 1*sin(u) Y(u,v,t)= 1.1*cos(u) Z(u,v,t)= 0.39*u^3
X(u,v,t)= 1*sin(u) Y(u,v,t)= 1.1*cos(u) Z(u,v,t)= 0.41*u^3
X(u,v,t)= 1*sin(u) Y(u,v,t)= 1.1*cos(u) Z(u,v,t)= 0.43*u^3
minU: -10,
maxU: 10,
Steps: 100