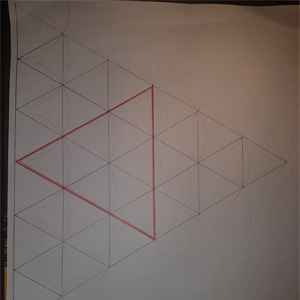
Zadatak je napraviti jedan primer (modul) papirnog fraktala i/ili kompozicije papirnih fraktala.
Iterativnim ponavljanjem afinih transformacija papira (savijanje, zasecanje itd.), nastaje papirni fraktal (paper folding fractal).
Priložiti jednu jasnu kadriranu fotografiju veličine 300x300 piksela izabranog modula ili do najviše tri fotografije zadatih veličina u slučaju prikaza generatora, n-te iteracije i/ili kompozicije. Takođe, u tekstualnom delu odgovora rečima opisati/formulisati pravilo/algoritam po kome je fraktalna forma generisana.
Zadatak traje nedelju dana, tačnije do 24.decembra do 22.45h.
Da bi zadatak bio adekvatno ocenjen, neophodno je na čas, u utorak 17.decembra, doneti potreban materijal (papire, karton, makaze itd.) i realizovati zadatak i na samom času. Fotografisaćemo najuspešnije modele.
Primer:
Prikazani modul nastaje po sledećem algoritmu: papir kvadratnog oblika saviti na pola, zasecati po sredini savijene ivice do pola, jedan od zasečenih delova presaviti paralelno dužoj stranici.

Kombinacijom ovako dobijenih modula dobija se sledeća prostorna kompozicija:













































 Prikazani model se dobija na sledeci nacin:
Prikazani model se dobija na sledeci nacin:











































































































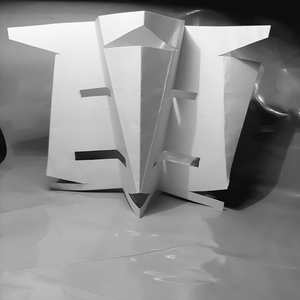
















































































































































 forma.
forma.











 Prikazani fraktal nastaje tako sto papir poprecno podeli na sto manje delove a onda tako prethodno savijen se deli na jos manje trouglove koji se zatim uvlace odnosno izbacuju kako bi dali cik cak izgled
Prikazani fraktal nastaje tako sto papir poprecno podeli na sto manje delove a onda tako prethodno savijen se deli na jos manje trouglove koji se zatim uvlace odnosno izbacuju kako bi dali cik cak izgled