Prvi domaći - projektivna preslikavanja, do 29.10. u 12:00

Standardni i DLP algoritam, resenje

 
Slika Tester Testerovic
Standardni i DLP algoritam, resenje
napisao/la Tester Testerovic - ponedeljak, 15. oktobar 2018, 12:15
 

Student: Tester Testerović, 273/91

Programski jezik: Mathematica 7.0

Uradjeno: Naivni algoritam, DLT algoritam, poredjenje algoritama na 4 tačke, analiza uticaja šuma na rezultat

Prilog: slika koda, 2 slike sa test primerom i poredjenjem algoritama (3 ukupno)

Zapažanja:

  1. Na 4 tačke naivni i DLT algoritam su se poklapali u potpunosti.
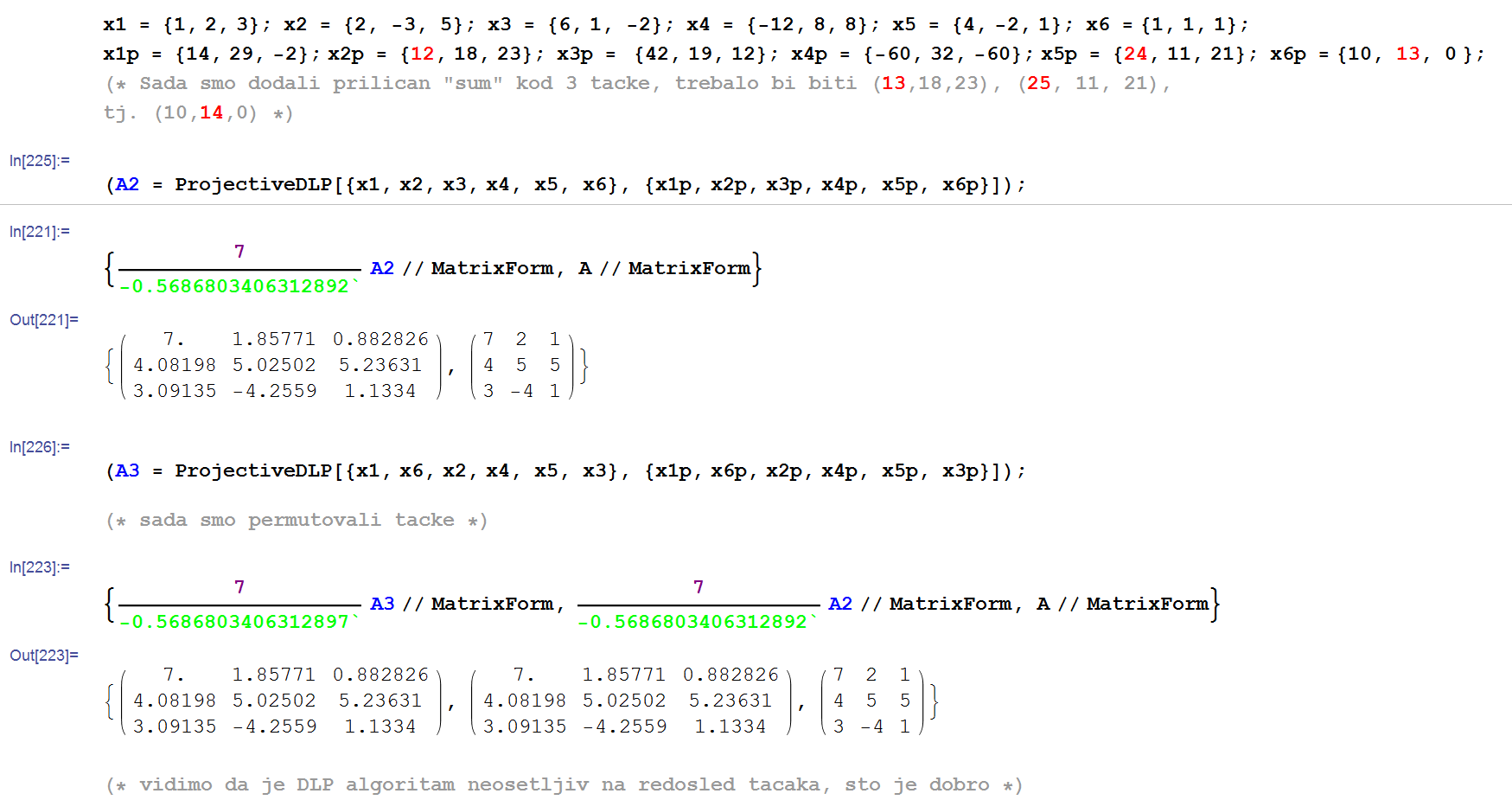
  2. Kada sam upotrebio DLT za 6 tačaka (dodao šum na 1 tački), ništa se nije promenilo.
  3. Kada sam da dodao šum na 3 tačke, a preostale 3 tačke su bile tačne, rezultat se promenio, ali je ostao u suštini "sličan".
  4. DLT algoritam ne zavisi od redosleda tačaka.

 
Permanentni link
Slika Boris Karanovic
Odgovor: Standardni i DLP algoritam, resenje
napisao/la Boris Karanovic - petak, 26. oktobar 2018, 22:59
 
Postovani profesore,
Uspesno sam uradio naivni i obican DLT algoritam, ali imam problem sa normalizovanim. Iz materijala nisam siguran da sam dobro shvatio proces normalizacije, pa cu izneti kako sam ga shvatio da vidite da li je dobro:
 
1) Izracunati teziste : T(Tx, Ty, Tz) gde je Tx = (Ax + Bx + .. + Dx) / 6 i tako za svaku koordinatu Tx, Ty, Tz
2) T(Tx, Ty, Tz) = (Tx/Tz, Ty/Tz, 1) // Ovde sam podelio sa Tz da bih se vratio u euklidsku ravan
3) Translirati T u koord pocetak:
            |   1   0  -Tx |
            |   0   1  -Ty |
            |   0   0    1  |
4) Skalirati tacke tako da prosecna udaljenost tacke od koordinatnog pocetka bude √2
      - sqrt ( x^2 + y^2  )    gde je x = Ax i y = Ay, tj ovo je euklidsko rastojanje tacke do koord pocetka
      - Sumiram sve te vrednosti i podelim sa brojem tacaka (6) i dobijemo neku vrednost avg
      - Matrica skaliranja:
            |   √2/avg   0   0 |
            |   0   √2/avg   0 |
            |   0      0        0 |
      - √2/avg sam koristio da bih nesto sa razdaljine avg doveo na razdaljinu √2 prilikom mnozenja
5) Zatim G =S * T i dalje nastavljam sa algoritmom.
 
Da li je mozda problematican korak 2 ? Njega sam primenio da bi mi poslednji element u matrici T bio 1.
 
 
Permanentni link | Prikaži nadređenu poruku
Slika Srdjan Vukmirovic
Odgovor: Standardni i DLP algoritam, resenje
napisao/la Srdjan Vukmirovic - petak, 26. oktobar 2018, 23:15
 

Prepostavljamo da su sve koordinate konacne (tj. Tz nije nula). Vi ste stavili 6, ali to treba da bude broj tacaka koje koristite.

Ako je A(Ax,Ay), B(Bx, By).... onda je T(Tx,Ty) = (Ax + Bx + ...., Ay + By + ....)/n  , gde je n broj tacaka. Dakle teziste racunamo u afinim koordinatama (moze i u homogenim ako je treca koordinata svih tacaka jednaka 1).

Translacija je dobra.

Dobijate translirane tacke A(Ax1, Ay1), B(Bx1, By1).... i ZA NJIH  odredjujete rastojanje od koord. pocetka.

Sve vam je dobro u koraku 4, ali treba da bude elemenat matrice skaliranja na poziciji (3,3) jednak 1, a ne 0!

 

 

 
Permanentni link | Prikaži nadređenu poruku