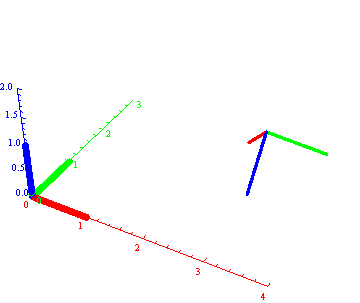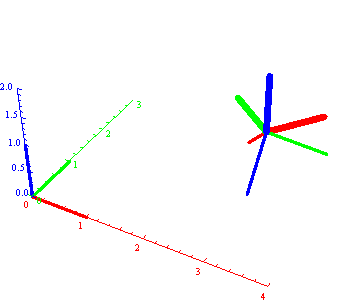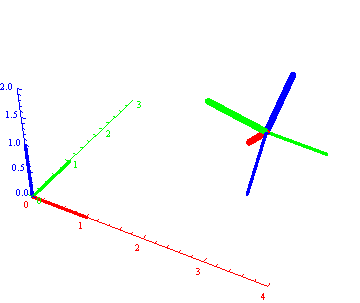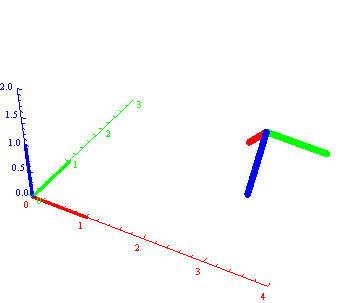
Ova animacija nije domaći. Ona prikazuje kako je svaki objekat (u ovom slučaju reper) moguće dovesti u proizvoljan položaj translacijom i trima sopstenim rotacijama.
Dakle položaj objekta je odredjen pozicijom centra (tj. novog koord. početka, ovde C1(3,2,1)) i "orjentacijom", u ovom slučaju zadatom trima Ojlerovim uglovima (ovde 7 Pi/6, Pi/4, 3 Pi /4). Taj reper će biti prvi objekat u animaciji koja sledi.
Dakle sada zadajemo i drugi objekat centrom C2(3/2, 0, 0) i Ojlerovim uglovima: Pi/2, -Pi/3, 5 Pi/4.
Prebacujemo prve i druge Ojlerove uglove u matrice, a zatim u kvaternione.
Prvom objektu odgovara "orjentacija", tj. kvaternion q1 = (0.433013, 0.786566, -0.362372, 0.25), a drugom q2 = (-0.092296, -0.701057, -0.430459, 0.560986).
"Orjentaciju" interpoliramo SLerp metodom, a položaj centra linearno, tj. C(t) = (1-t)C1 + t C2 i dobijamo sledeću animaciju (koja jeste domaći).
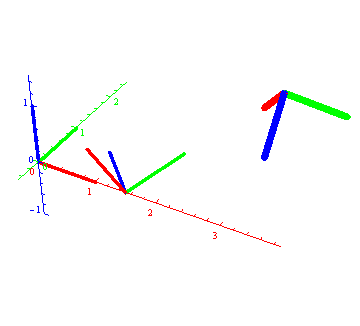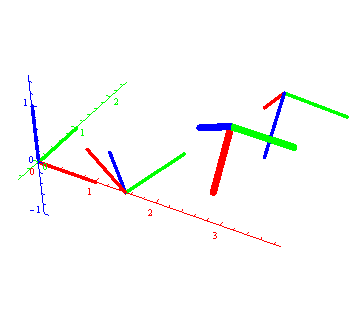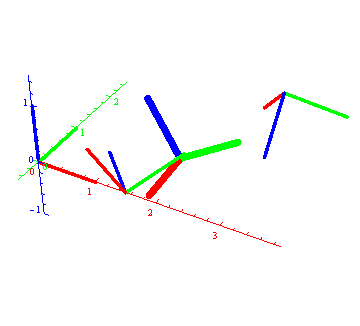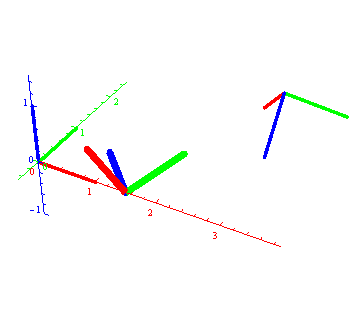
Animacije su lošeg kvaliteta jer sam zbog uštede prostora i portabilnosti koristio "animated gif."