Student: Branko Djakovic, 41/2015
Programski jezik: Python2.7 uz dodatne biblioteke numpy i matplotlib.
Uradjeno:
- Naivni, DLT i normalizovani DLT algoritam.
- Poredjenje algoritama za razliciti broj tacaka
- Zapazanja kako sum i permutacija tacaka uticu na algoritme
- Unos tacaka putem datoteke
- Graficki prikaz ulaznih i izlaznih tacaka iskazanih kao poligoni
U datoteku unesem zeljene tacke u obliku x,y,z i poretku A,B,C ... Ap,Bp,Cp gde svaka ide u razlicit red. Ukoliko ima vise od 4 tacke naivni algoritam se radi za prve 4 tacke i prve 4 slike. Rezultati se dobijaju na standardni izlaz uz iscrtavanje slika u dva nova prozora (na jednom se iscrtava za 4 tacke, na drugom za sve)
Prilog:
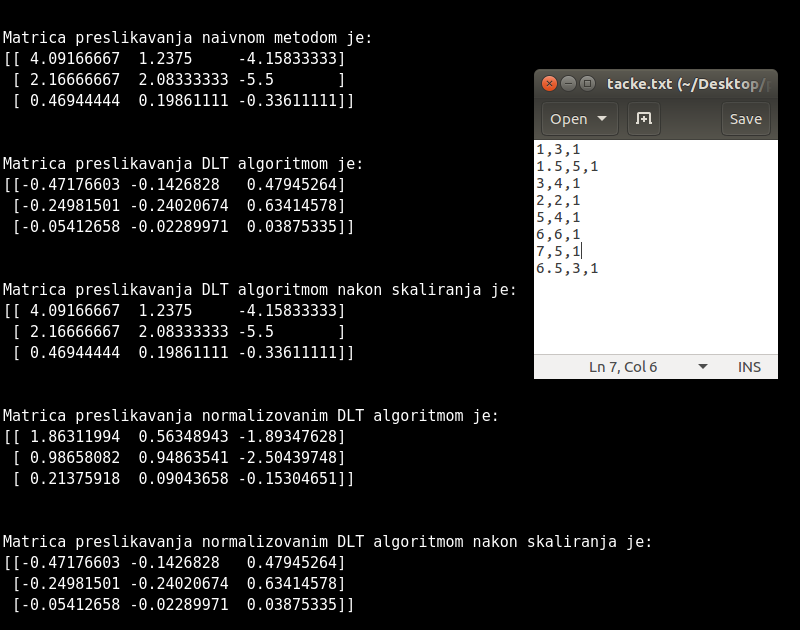
- Prikaz matrice preslikavanja za sva tri algoritma kada se koriste 4 tacke kao i datoteka sa tackama koje su koriscene
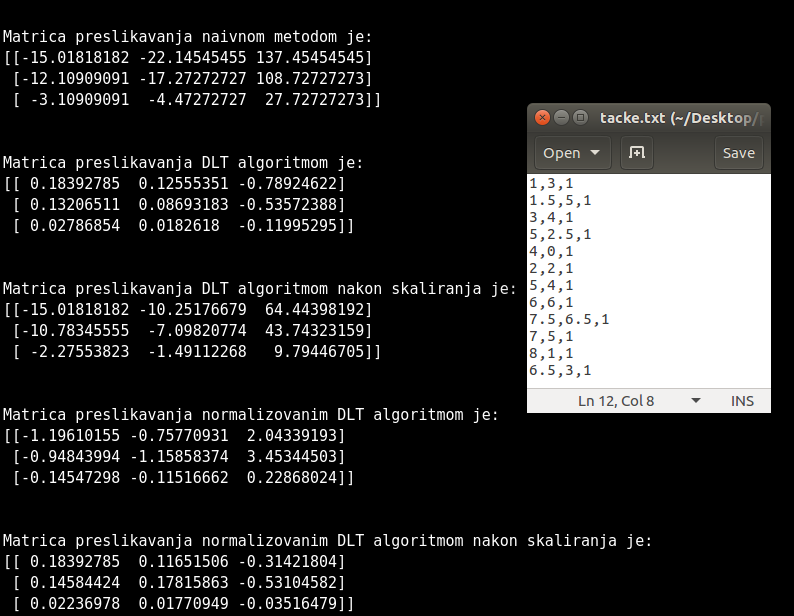
- Prikaz matrice preslikavanja za sva tri algoritma kada se koristi 6 tacaka kao i datoteka sa tackama koje su koriscene (za naivni se koriste prve cetri tacke)
- Prikaz poligona koriscenih tacaka kada je u pitanju 6 tacaka i 4 tacke
- Deo koda kada se ucitavaju tacke i pokrecu algoritmi i vrsi provera kolinearnosti i normalizacija
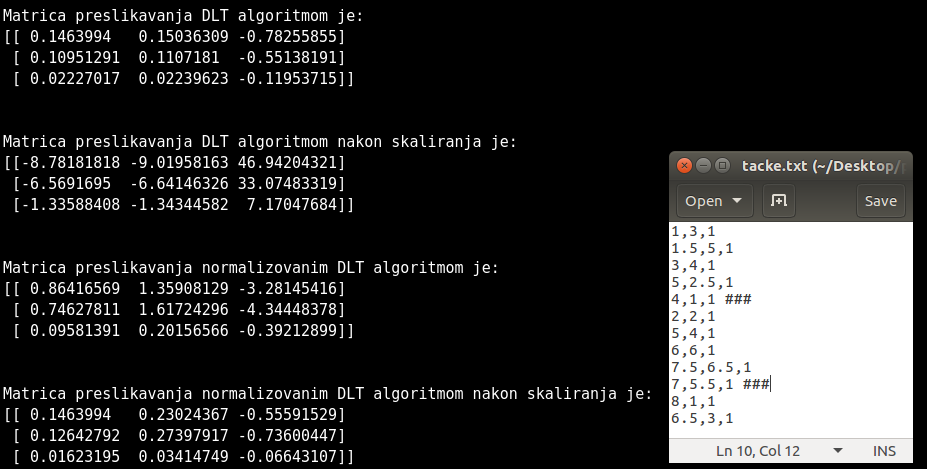
- Prikaz izlaza sa 6 tacaka kada se doda sum
- Prikaz izlaza sa 6 tacaka kada se permutuju tacke
Zapazanja:
Kada je u pitanju 4 tacke algoritmi daju ista resenja a kada se posmatra vise tacaka DLT i normalizovani DLT daju veoma bliska resenja dok naivni daje dosta razlicita, Dodavanje suma na tacke E i Dp je dovelo do razlike u matricama preslikavanja ali je rezultat idalje blizak pravom. Permutovanje tacaka ne utice na DLT i normalizovani DLT sto se vidi u prilogu gde je izvrsena permutacija tacaka E i F i Ep i Fp.
Tacke:
A = [1,3]
B = [1.5,5]
C = [3,4]
D = [5,2.5]
E = [4,0] sa sumom E = [4,1]
F = [2,2]
Ap = [5,4]
Bp = [6,6]
Cp = [7.5,6.5]
Dp = [7,5] sa sumom Dp = [7,5.5]
Ep = [8,1]
Fp = [6.5,3]