Filip Jovasevic 142/2015
Kod je pisan u programskom jeziku Python, uz koriscenje biblioteka numpy, matplotlib i math
Implementirao sam naivni, DLT i normalizovani DLT algoritam i vrsio analizu i poredjenje resenja algoritama.
Algoritme sam primenjivao za 4 i 6 tacaka.
Graficki sam predstavio ulazne i izlazne tacke algoritma.
- A = ( 1, -5 )
- B = ( -1,-7)
- C = (5, -6.2)
- D = (6.5, -3)
- E = ( 4.2, 0)
- F = ( 0, 4 )
- Ap =(10, 13 )
- Bp =(6, 9 )
- Cp =(7, 6.4 )
- Dp =(9, 5 )
- Ep =(10, 9 )
- Fp =(13.5 , 7.5 )
Za naivni, DLT i normalizovani DLT algoritam sa 4 tacke sam uzeo prve 4 tacke.
Po pokretanju programa neophodno je uneti koordinate tacaka i njihovih slika preko terminala. U zavisnosti od odabranog algoritma za izvrsavanje u terminalu dobijamo izlaznu matricu preslikavanja.
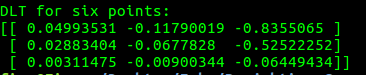
Ono sto sam uocio jeste da se primenom normalizovanog DLT algoritma na 6 tacaka nakon skaliranja ne dobije isti rezultat kao i primenom obicnog DLT algoritma, sto jeste slucaj za 4 tacke, jer povecanjem broja tacaka raste i velicina greske. Promenom redosleda tacaka nije doslo do promena, sto znaci da je algoritam nezavistan od redosleda tacaka.
Na slikama su prikazana resenja za pomenute algoritme u zavisnosti od broja tacaka(4 ili 6).